Pitanja za usmeni ispit iz OAU-a kod profesora Sliškovića

Analiza 1 (modeli procesa i osnovni oblici dinamičkog vladanja)

1. Modeliranje procesa (izgradnja modela kroz teorijsku analizu)
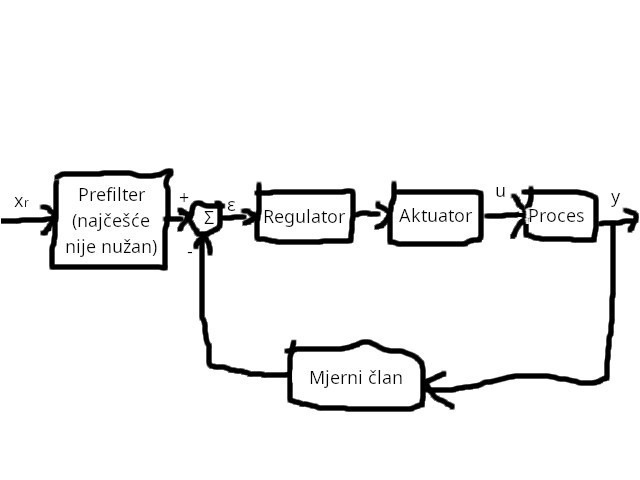
   Za modeliranje linearnih mehaničkih sustava, koristimo Newtonove zakone. Za modeliranje rotacijskih mehaničkih sustava, koristimo zakone inercije. Za modeliranje električnih sustava s koncentriranim parametrima, koristimo Kirchhoffove zakone. Za modeliranje električnih sustava s raspodjeljenim parametrima, koristimo Maxwellove jednadžbe.
2. Linearnost/nelinearnost (dinamičkih) sustava; linearizacija, zašto i kako se provodi
   Linearni sustav znači da za njega vrijedi princip superpozicije, da odziv na kompleksnu pobudu bude jednak zbroju odziva na pobude od kojih je ta kompleksna pobuda sastavljena. Svaki je realni sustav više ili manje nelinearan. Linearizacija je aproksimacija nelinearnog sustava oko neke radne točke linearnim sustavom. Ona se provodi preko parcijalnih derivacija: \[ \frac{dy}{dt}=f[y(t),x(t)] \] \[ \frac{d \Delta y}{dt} = \frac{\partial f[y(t),x(t)]}{\partial x}|_0 * \Delta x(t) + \frac{\partial f[y(t),x(t)]}{\partial y}|_0 * \Delta y(t) \] Linearizacija se provodi zato što za linearne sustave postoji zaokružena teorija o analizi i sintezi takvih sustava, dok za nelinearne ne postoji.
3. Opis sustava pomoću specijaliziranih signala (prijelazna i težinska funkcija, veza između njih, te njihova veza s prijenosnom funkcijom)
   Prijelazna funkcija, \( h(t) \), je odgovor na step pobudu, jediničnu stepenicu, \( S(t) \). Step-funkcija izgleda ovako:
   
   Težinska funkcija, \( g(t) \), je odgovor na Dircovu delta funkciju, \( \delta(t) \). Diracova delta funkcija je derivacija step pobude po vremenu. Ona je jednaka nuli u svim točkama na realnoj osi osim u nuli, a u nuli je \( \infty \). Integral Diracove delta funkcije u svakom intervalu koji uključuje nulu jednak je jedinici.
   
   Za linearne sustave, težinska funkcija je derivacija prijelazne funkcije po vremenu: \[ g(t)=\frac{d h(t)}{dt} \] Izraz "prijenosna funkcija", \( G(s) \), ima dva značenja:
   1. Laplaceova transformacija težinske funkcije: \[ G(s)=ℒ\{g(t)\} \]
   2. Omjer izlaza i ulaza u Laplaceovoj domeni: \[ G(s)=\frac{Y(s)}{X(s)} \]
   U linearnim sustavima, te su dvije definicije iste.
4. Dinamički član s PT₂ vladanjem; opis u t, s i ω-području (za svih pet slučajeva PT₂-vladanja), primjer sustava s ovakvim vladanjem.
   PT₂ član ima ovakvu prijenosnu funkciju: \[ G(s)=K \frac{1}{\frac{s^2}{\omega_n^2} + \frac{2\zeta}{\omega_n}s + 1}\] O vrijednosti ζ ovisi gdje će se nalaziti polovi sustava i hoće li sustav biti stabilan. Ako je \( \zeta = 1 \), to znači da sustav ima dva realna pola lijevo od imaginarne osi oba na istom mjestu (dakle, jedan dvostruki realni pol). Tada njegova prijelazna funkcija izgleda ovako:
   
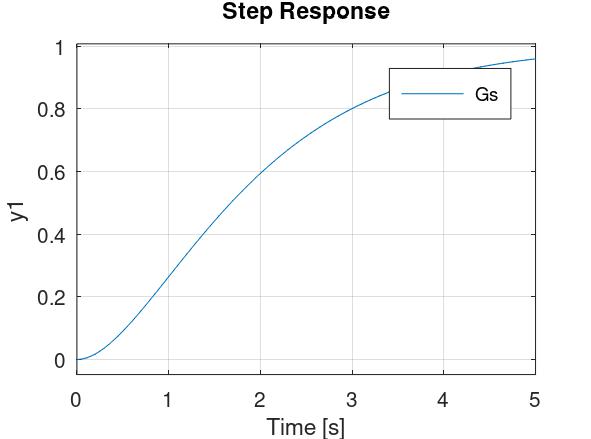
   Ako je \( \zeta > 1 \), to znači da sustav ima dva realna pola na različitim mjestima. I što je ζ veća, to je udaljenost između ta dva pola isto veća. Za \( \zeta = 5 \), prijelazna funkcija izgleda ovako:
   
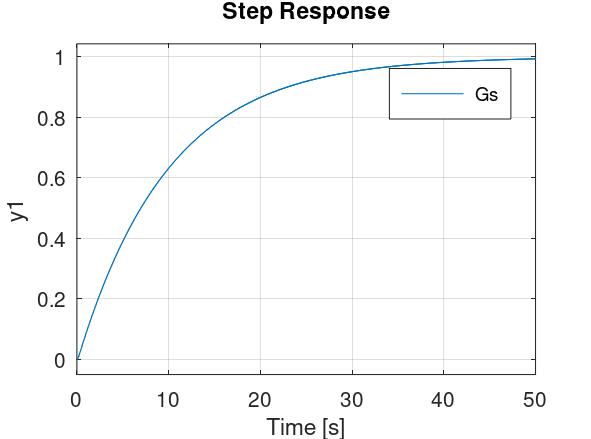
   (Primijetite razliku u redu veličine na apscisi!)
   Ako je \( 0 < \zeta < 1 \), to znači da su polovi konjugirano kompleksni i u lijevoj poluravnini (lijevo od imaginarne osi), pod kutom u odnosu na negativni dio realne osi \( \alpha = \arccos(\zeta) \). Za \( \zeta = \frac{\sqrt{2}}{2} \) (dakle, da su polovi pod kutem od \( \alpha = \arccos ( \frac{\sqrt{2}}{2} ) = 45^{\circ} \) u odnosu na realnu os), prijelazna funkcija izgleda ovako:
   
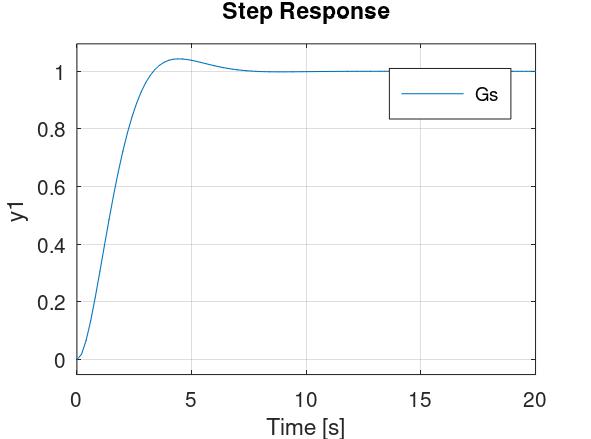
   I što je ζ manji (a α veći), to su polovi bliže imaginarnoj osi, i time je sustav oscilatorniji. Primjerice, za \( \zeta = 0.1 \), prijelazna funkcija izgleda ovako:
   
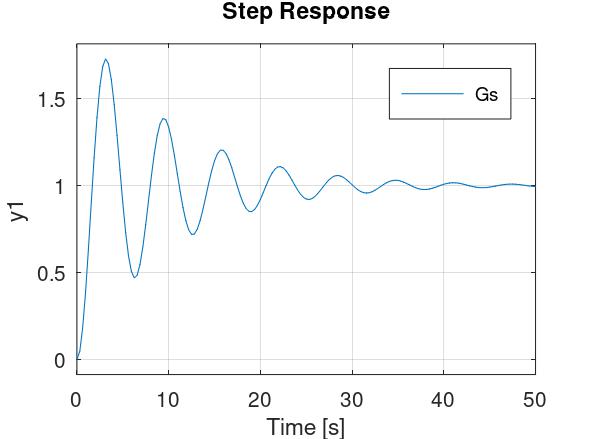
   Kad je ζ jednak nuli (a α 90^o), tada su polovi na imaginarnoj osi, i prijelazna funkcija je sinusoida amplitude 1 pomaknuta za 1 prema gore i frekvencije ω_n:
   
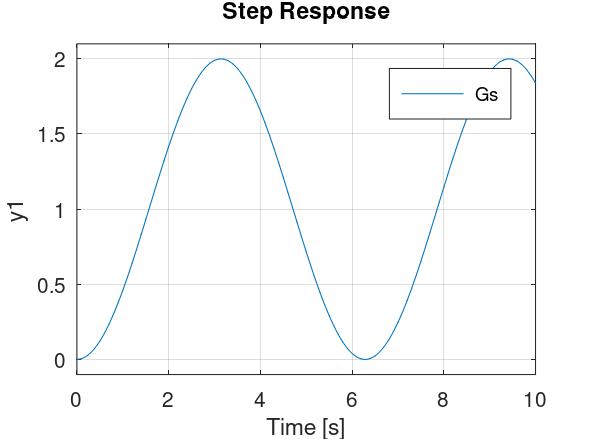
   Kada je \( \zeta > 0 \), tada su polovi s desne strane imaginarne osi, i oscilacije rastu (teoretski) u beskonačno, što će uništiti sustav:
   
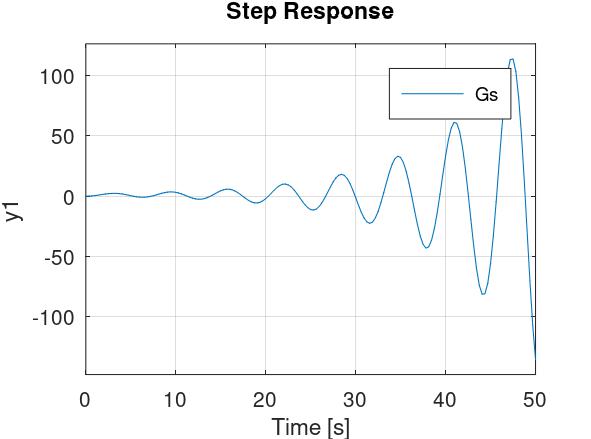
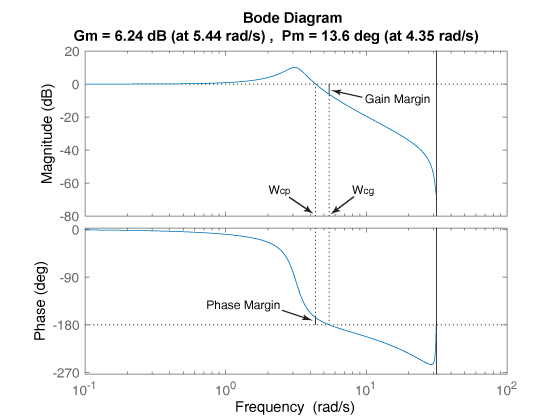
   Bodeov dijagram (pretpostavljam da je to ono što profesor misli pod ω-domenom) PT₂-člana izgleda ovako (preuzeto od Malgorzate Zywno):
   
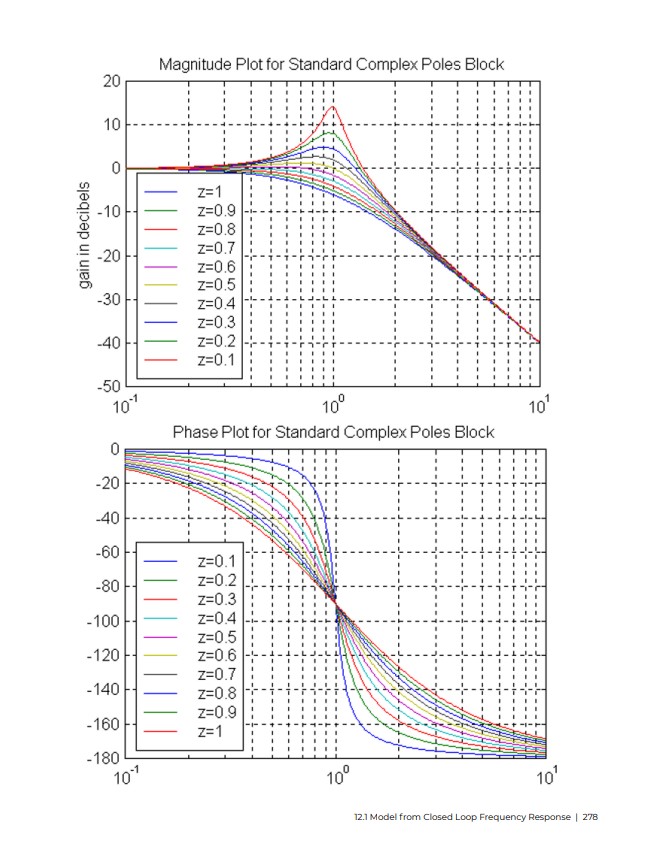
   (Malgorzata Zywno prigušenje označava sa z umjesto sa ζ.)
   Primjer sustava s PT₂ vladanjem je serijski RLC krug:
   
   Označimo s u₂ napon na kondenzatoru, a s u₁ napon na izvoru. Onda je diferencijalna jednadžba tog kruga: \[ LC\frac{d^2u_2}{dt^2}+RC\frac{du_2}{dt}+u_2=u_1 \]
5. Dinamički član s IT₁-vladanjem; opis u t, s i ω-području, primjer sustava s ovakvim vladanjem
   IT₁-član ima prijenosnu funkciju: \[ G(s)=\frac{K}{T_Is(Ts+1)} \] Prijelazna funkcija izgleda ovako (ovo ispisuje Octave na step(1/(s*(s+1)))):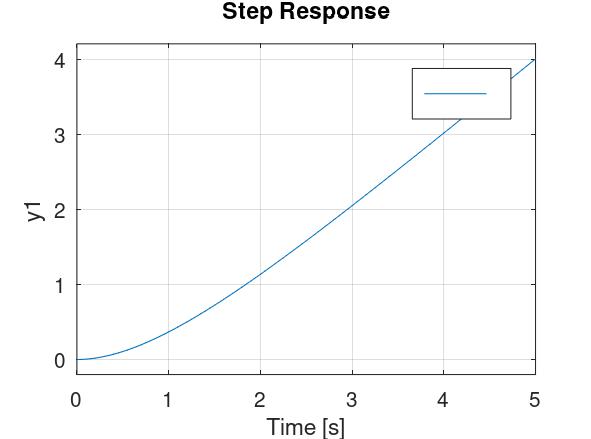
   
   Bodeov dijagram izgleda ovako (ovo ispisuje Octave na bode(1/(s*(s+1)))):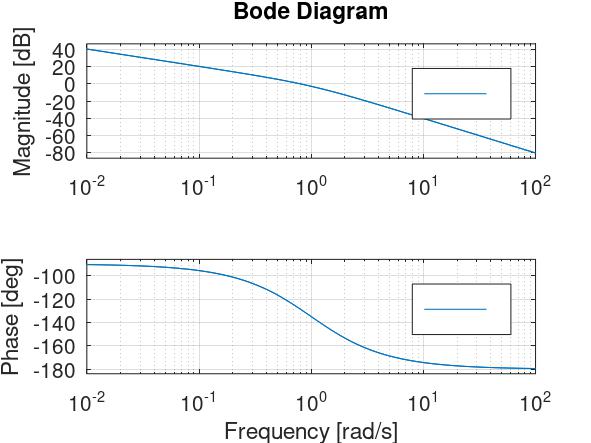
   
   U Periću na 108. stranici u tablici ima ovaj primjer sustava s IT₁ vladanjem:
   
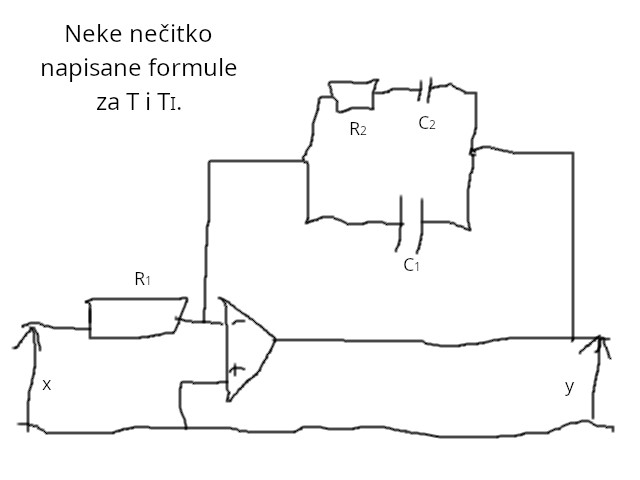
   (UPDATE: Rekao mi je profesor na konzultacijama da je primjer sustava s IT₁ vladanjem spremnik bez rupe na dnu s ventilom, jer je sam spremnik bez rupe I-član, a ventil je PT₁-član.)
6. Dinamički član s PI-vladanjem; opis u t, s i ω-području, primjer sustava s ovakvim vladanjem
   PI-član ima ovakvu prijenosnu funkciju: \[ G(s)=K\left( 1+\frac{1}{T_Is}\right) \] Mnogi su regulatori PI-regulatori, oni se koriste kad je točnost u stacionarnom stanju važna (što se ne može postići P-regulatorom).
   Njegova prijelazna funkcija izgleda ovako (ovo ispisuje Octave na step(1+1/s)):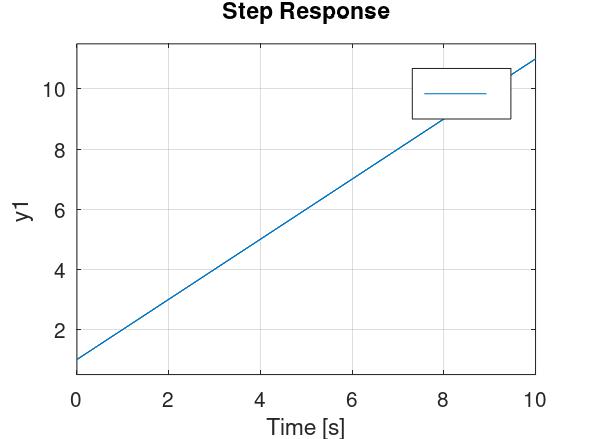
   
   Njegov Bodeov dijagram izgleda ovako (ovo ispisuje Octave na bode(1+1/s)):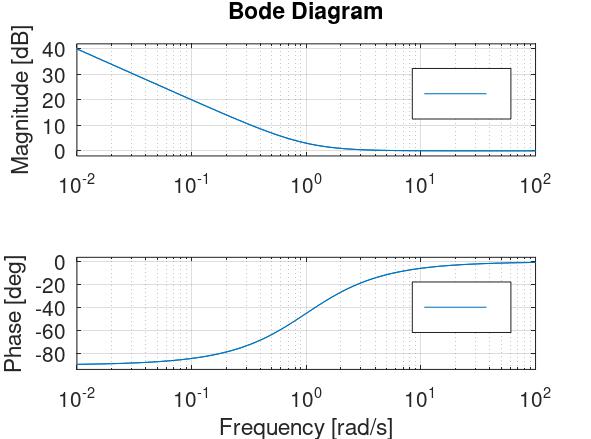
   
   
7. Dinamički član s PID/PIDT₁-vladanjem; opis u t, s i ω-području, primjer sustava s ovakvim vladanjem
   Idealni PID-član ima ovakvu prijenosnu funkciju: \[ G(s)=K\left(1+\frac{1}{T_Is}+T_Ds\right) \] Realni PID-član (pretpostavljam da je to ono što profesor misli pod PIDT₁) ima ovakvu prijenosnu funkciju: \[ G(s)=K\left(1+\frac{1}{T_Is}+\frac{T_Ds}{1+T_Vs}\right), T_V \ll T_D \] Bode dijagram PID-člana je (ovo Octave ispisuje ako joj se zada bode(1*(1+1/s+s))):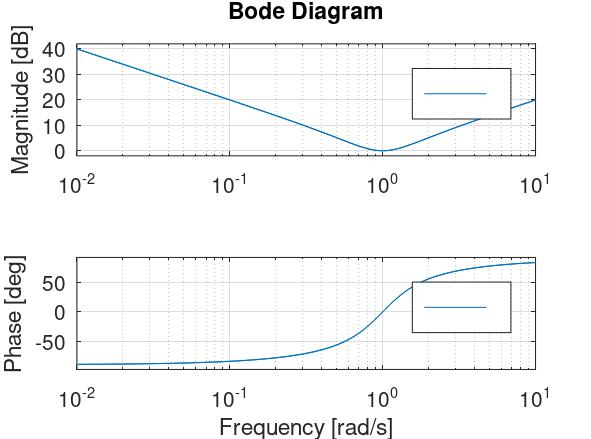
   
   Joško Petrić (stranica 170) kaže da su taj špic prema dolje u amplitudnoj karakteristici i točka gdje je fazna karakteristika u nuli na frekvenciji \( \frac{1}{\sqrt{T_IT_D}} \).
   Kao da se sjećam da sam negdje vidio da je prijelazna funkcija idealnog PID-člana ovakva:
   
   PID-član se često koristi kao regulator, jer se njime postiže brz odziv i točnost u stacionarnom stanju. Problem s PID-regulatorom je što ga je komplicirano postaviti.
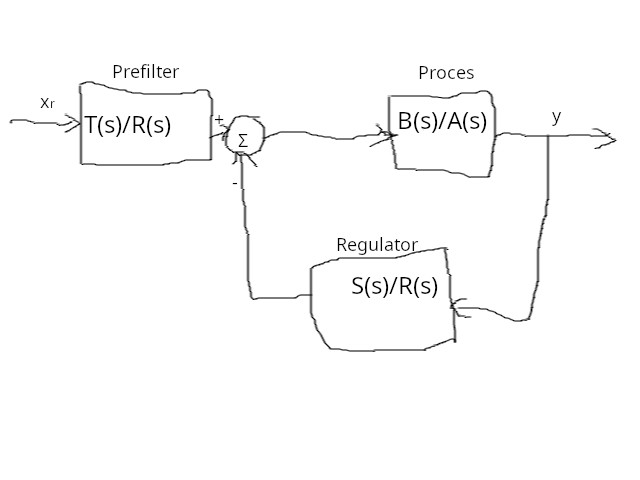
   Primjer približne realizacije PID regulatora (a on se ne može egzaktno realizirati) je ovo:
   
8. Dinamički članovi s faznim prethođenjem (LEAD) i faznim kašnjenjem (LAG); opis u t, s i ω-području, primjer sustava s ovakvim vladanjem
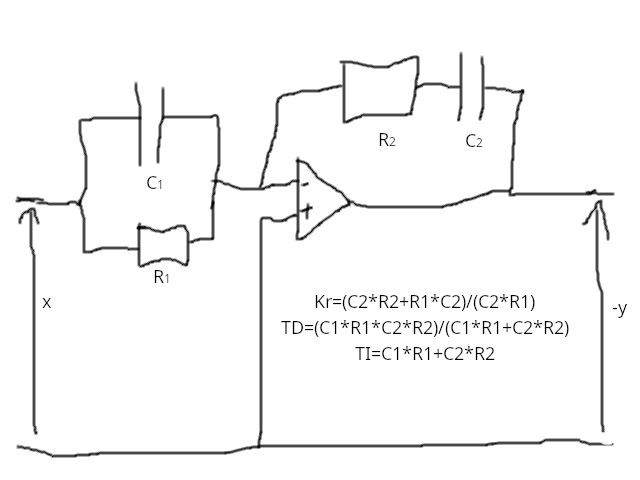
   Član s faznim prethođenjem ima prijenosnu funkciju: \[ G(s)=\frac{1+Ts}{1+\alpha Ts}, 0<\alpha<1 \] Korekcijski član s faznim prethođenjem služi za podizanje fazne karakteristike u određenom frekvencijskom području. Njegov Bodeov dijagram izgleda ovako (nacrtano u Octavi):
   
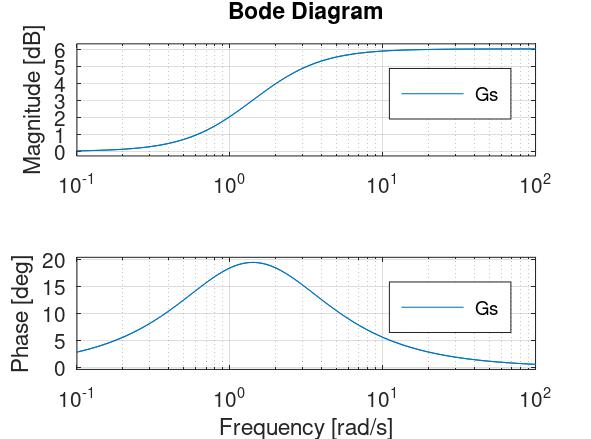
   On na višim frekvencijama podiže amplitudnu karakteristiku za \( \frac{1}{\alpha} \), što je obično nepovoljno (jer se na visokim frekvencijama obično nalazi šum, a ne signal).
   Ako se dobro sjećam, član s faznim kašnjenjem ima istu tu prijenosnu funkciju, samo je α u nekom drugom intervalu, ali ne mogu sad to naći (UPDATE: Rekao mi je profesor na konzultacijama da je za LAG član α veća od 1.).
   Članove s faznim prethođenjem i faznim kašnjenjem možemo realizirati ovako (pojma nemam što znači ω_ζ i ω_κ):
   
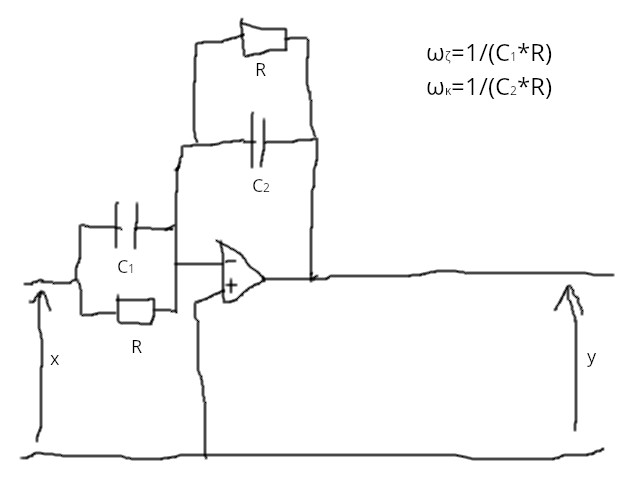
   (UPDATE: Rekao mi je profesor na konzultacijama da je LEAD isto što i PDT₁.)
9. Dinamički članovi s T_t i T_tT₁-vladanjem (PT₁T_t); opis u t, s i ω-području, primjer sustava s ovakvim vladanjem
   T_t znači "član s mrtvim vremenom", kad je \( y(t)=x(t-T_t) \). t dolazi od njemačkog tot (mrtav). Njegova prijenosna funkcija glasi: \[ G(s)=e^{-T_ts} \] Njegov Bodeov dijagram izgleda ovako (preuzeto od Emilija Frazzolija, pokušao sam napraviti svoj, ali Octave mi javlja nekakvu poruku o pogrešci):
   
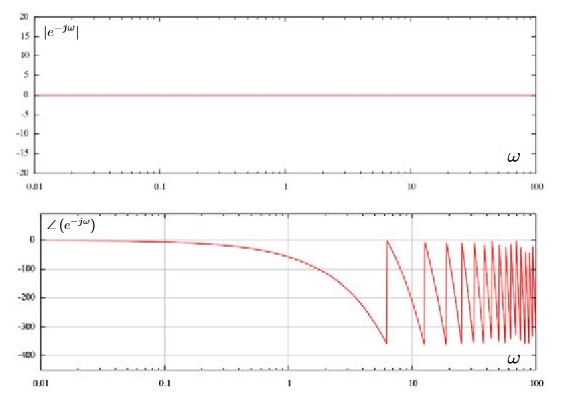
   Takvo vladanje ima, recimo, transportna traka koja prenosi neki materijal. Takva su vladanja jako rijetka u električnim i elektroničkim sustavima, ali su česta u mehaničkim.

Analiza 2 (regulacijski krug i njegova svojstva/karakteristike)

1. Standardni tipovi regulatora (PID i iz njega izvedeni tipovi), opis u t, s i ω-području
   Za opis u t, s i ω-području, vidi pitanje 1.7.
   Standardni tipovi regulatora su:

   Tip regulatora	Prednosti	Nedostatci
   P-regulator	Jednostavno podešavanje Relativno brza reakcija na poremećaj i promjenu vodeće veličine.	Veliko odstupanje u stacionarnom stanju. Ne može stabilizirati neke sustave koje PD i PID mogu.
   PD-regulator	Brza reakcija na poremećaj i promjenu referentne veličine Može stabilizirati neke sustave koje P, I i PI ne mogu (tako što izobličuje krivulju mjesta korijena prema lijevo).	Odstupanje u stacionarnom stanju Ne može se egzaktno realizirati.
   I-regulator	Točnost u stacionarnom stanju	Spora reakcija na poremećaj i promjenu referentne veličine Ne može stabilizirati neke sustave koje PD i PID mogu.
   PI-regulator	Točnost u stacionarnom stanju. Relativno brza reakcija na poremećaj. Relativno jednostavno podešavanje.	Ne može stabilizirati neke sustave koje PD i PID mogu.
   PID-regulator	Točnost u stacionarnom stanju Brza reakcija na poremećaj Može stabilizirati sustave koji P, I i PI ne mogu	Kompliciran za podesiti. Ne može se egzaktno realizirati

2. Regulacijski krug; struktura regulacijskog kruga i uloga pojedinih elemenata, osnovne veličine u regulacijskom krugu, vladanje regulacijskog kruga s obzirom na vodeću i poremećajnu veličinu, prijenosne funkcije regulacijskog kruga i karakteristični polinom
   Vidi ovu sliku:
   
   Elementi regulacijskog kruga su:
   • Prefilter - služi za to da smanji nadvišenje pri skokovitim promjenama referentne veličine x_r, obično nije potreban
   • Regulator - implementira algoritam upravljanja procesom čiji je ulaz regulacijsko odstupanje ε
   • Aktuator - pretvara izlaz regulatora (danas najčešće digitalni električni signal) u fizičku veličinu kojom se upravlja procesom
   • Proces - ono čime želimo upravljati
   • Mjerni član - mjeri izlaz iz procesa y, pretvara ga u oblik razumljiv regulatoru (danas najčešće digitalni električni signal)
   Osnovni signali u regulacijskom krugu su:
   • x_r - referentna veličina (koliko želimo da bude y)
   • ε - regulacijsko odstupanje (ako nema prefiltra, onda vrijedi \( \epsilon = x_r - y \) )
   • u - upravljačka veličina
   • y - veličina kojom upravljamo
   • z - šum (smetnja)
   U idealnom slučaju, vladanje s obzirom na smetnju je \( \frac{Y(s)}{Z(s)}=0 \), a vladanje s obzirom na vodeću (referentnu) veličinu je \( \frac{Y(s)}{X_r(s)}=1 \). To, naravno, nije moguće postići. Ali, s obzirom na to da je smetnja najčešće visoke frekvencije, a vodeća veličina niske frekvencije, možemo napraviti da prijenosna funkcija ima što veću vrijednost za niske frekvencije, a što manju za visoke.
   Regulacijski krug ima prijenosnu funkciju otvorenog regulacijskog kruga \( G_O(s)=G_R(s)G_s(s) \), gdje je G_R prijenosna funkcija regulatora, a G_S(s) prijenosna funkcija procesa, te ima prijenosnu funkciju zatvorenog regulacijskog kruga G_x(s). Ako je prijenosna funkcija mjernog člana jednaka jedinici (što u realnosti nikad nije, ali u idealnom slučaju jest), onda vrijedi formula: \[ G_x(s)=\frac{G_O(s)}{1+G_O(s)} \] Karakteristični polinom je nazivnik od G_x.
3. Negativna povratna veza - njezine dobre i loše strane, primjeri
   Negativna povratna veza znači da mjerimo izlaz iz sustava i da reagiramo na odstupanje njega od željene vrijednosti. Bez negativne povratne veze, možemo reagirati samo na smetnje koje smo unaprijed predvidjeli. S povratnom vezom možemo kompenzirati sve smetnje, i one koje nismo predvidjeli. To je glavna prednost povratne veze. Nedostatak povratne veze je što lošim odabirom regulatora možemo stabilan sustav učiniti nestabilnim (ako su svi polovi otvorenog regulacijskog kruga lijevo od imaginarne osi, ali neke grane krivulje mjesta korijena sijeku imaginarnu os).
   Primjer za negativnu povratnu vezu jest tempomat: on održava brzinu automobilna stalnom tako što smanjuje gas ako brzinomjer pokazuje preveliku brzinu, a pojačava gas ukoliko tempomat pokazuje premalu brzinu.
4. Statičke karakteristike regulacijskog kruga (analiza točnosti regulacijskog kruga); primjer analize točnosti za različite tipove regulacijskog kruga
   Statičke karakteristike regulacijskog kruga jesu pojačanje regulacijskog kruga i odstupanje u stacionarnom stanju. Pojačanje regulacijskog kruga jest omjer izlaza i ulaza u stacionarnom stanju. Drugim riječima, to je limes prijelazne funkcije kako vrijeme teži prema beskonačno: \[ K=\lim_{t \to +\infty} h(t) \] Točnost u stacionarnom stanju ovisi o vrsti sustava i o vrsti pobude. Sustav P-tipa ima odstupanje u stacionarnom stanju već i za step-pobudu. Sustav I-tipa nema odstupanje za step-pobudu, ali ima za pobudu u obliku rampe. Sustav I₂ tipa nema odstupanje ni za step-pobudu ni za pobudu u obliku rampe, ali ima za paraboličnu pobudu.
   Odstupanje u stacionarnom stanju može se odrediti preko teorema o konačnoj vrijednosti Laplaceove transformacije: \[ \lim_{t \to +\infty} e(t) = \lim_{s \to 0} sE(s) \] uzimajući u obzir da je Laplaceova transformacija step-funkcije \( \frac{X_{u0}}{s} \), rampe \( \frac{X_{u1}}{s^2} \), a parabolične pobude \( \frac{X_{u2}}{s^3} \).
   Primjerice, za sustav s P-vladanjem za skokovitu (step) pobudu vrijedi: \[ \lim_{t \to +\infty}e(t)=\lim_{s \to 0}s \cdot E(s)=\lim_{s \to 0}s\cdot\frac{1}{1+G_O(s)}\cdot X_u(s)=\lim_{s \to 0}s\cdot\frac{1}{1+K_o}\cdot\frac{X_{u0}}{s}=\frac{1}{1+K_o}X_{u0} \] Na usmenom ispitu sam rekao "Točnost u stacionarnom stanju ispitujemo tako da na sustav narimo step-pobudu i gledamo konvergira li odziv u jedinicu.", pa mi to profesor nije priznao. Tako da nemojte to reći.
5. Stabilnost regulacijskog kruga s negativnom povratnom vezom; definicija stabilnosti, uvjeti za nastupanje nestabilnosti, tipovi nestabilnosti, metode za analizu (ispitivanje) stabilnosti regulacijskog kruga
   Sustav je stabilan ako za svaku konačnu pobudu ima konačan odziv (bounded-input-bounded-output, BIBO). Linearni vremenski nepromjenjivi sustav je stabilan ako i samo ako njegova težinska funkcija (odziv na Diracov delta-impuls) konvergira u nulu: \[ \lim_{t \to +\infty}g(t)=0 \] Linearni vremenski nepromjenjiv sustav je stabilan ako i samo ako su svi njegovi polovi (korijeni nazivnika od G_x(s) ) lijevo od imaginarne osi. Ako ima polova na imaginarnoj osi, onda je na granici stabilnosti, a, ako je barem jedan pol desno od imaginarne osi (da ima pozitivan realni dio), onda je nestabilan. Za ispitivanje stabilnosti regulacijskog kruga postoje analitičke (Routh-Hurwitz) i grafičke metode (Bode, Nyquist).
   (UPDATE: Rekao mi je profesor na konzultacijama da su vrste nestabilnosti oscilatorna i monotona, te da je oscilatorna ako je ζ između nula i jedan, a monotona ako je ζ veća od jedan.)
6. Analitičke metode za ispitivanje stabilnosti regulacijskog kruga; što je objekt analize, što se dobije kao rezultat, osnovni i dodatni (nužni i dovoljni) uvjeti stabilnosti, algebarski kriteriji stabilnosti (praktični postupci), primjer (Hurwitz)
   Hurwitzov kriterij, ili njegov ekvivalent Routhov kriterij, analiziraju karakteristični polinom zatvorenog regulacijskog kruga. Kao rezultat dobije se broj polova desno od imaginarne osi (koji, da bi sustav bio stabilan, mora biti nula). To jest, dobijemo uvid u apsolutnu stabilnost (ne i relativnu). Nužan, ali ne i dovoljan, uvjet je da svi koeficijenti karakterističnog polinoma budu istog predznaka i različiti od nule. A dovoljan uvjet je da determinante sljedećih matrica budu pozitivne:

   a1

   a1	a0
   a3	a2

   a1	a0	0
   a3	a2	a1
   a5	a4	a3

   I tako dalje. Dakle, na glavnoj dijagonali nalaze se a₁, a₂, a₃, a₄, a₅, i tako dalje. A, kako idemo na lijevo, tako se indeks za svaku čeliju povećava. A, kako idemo na desno, tako se smanjuje.
   Implementirao sam Routhov kriterij (malo modificirani Hurwitzov kriterij) u svom programskom jeziku, možete ga isprobati u modernom internetskom pregledniku na mojoj web-stranici.
7. Grafo-analitičke metode za ispitivanje stabilnosti regulacijskog kruga; fizikalno objašnjenje uvjeta za nastupanje nestabilnosti i ruba stabilnosti, što je objekt analize u ovim metodama, relativna stabilnost i pokazatelji relativne stabilnosti, primjer
   Grafo-analitičke metode za ispitivanje stabilnosti regulacijskog kruga jesu Bodeov kriterij i Nyquistov kriterij. Oni analiziraju prijenosnu funkciju otvorenog regulacijskog kruga (a ne zatvorenog, kao Hurwitzov i Routhouv kriterij). Oba se temelje na činjenici da, na frekvenciji kad u procesu postoji kašnjenje od 180^o (to se zove protufaza), da bi sustav bio stabilan, pojačanje mora biti manje od 1.
   Nyquistov dijagram je krivulja u kompleksnoj ravnini gdje svaka točka predstavlja pojačanje i fazu za određenu frekvenciju. Udaljenost točke od ishodišta predstavlja pojačanje za tu frekvenciju, a kut u odnosu na pozitivni dio realne osi predstavlja fazu za tu istu frekvenciju. I ako ta krivulja siječe negativni dio realne osi desno od točke (-1, 0), onda je sustav stabilan. Ako je siječe točno u točki (-1, 0), onda je na granici stabilnosti, a ako je siječe lijevo od te točke, onda je sustav nestabilan. Primjerice, ovaj Nyquistov dijagram:
   
   Taj sustav je stabilan, jer krivulja siječe negativni dio realne osi desno od (-1, 0).
   Bodeov kriterij stabilnosti kaže da, da bi sustav bio stabilan, ω_c mora biti manje od ω_π. ω_c je frekvencija na kojoj amplitudna karakteristika siječe 0dB, a ω_π je frekvencija u kojoj frekvencijska karakteristika siječe -180^o (-π rad). Primjerice, ovaj Bodeov dijagram:
   
   Predstavlja stabilan sustav.
   Grafo-analitičke metode ne daju samo uvid u apsolutnu stabilnost, nego i u relativnu stabilnost. Relativna stabilnost je koliko smo udaljeni od ruba stabilnosti. Pokazatelji relativne stabilnosti su amplitudno i fazno osiguranje. Amplitudno osiguranje je za koliko smijemo povećati pojačanje da bismo dostigli rub stabilnosti. Fazno osiguranje, γ, iznos je faznog kašnjenja uz koje bismo dostigli rub stabilnosti.
   Amplitudno osiguranje može se očitati iz Nyquistovog dijagrama kao udaljenost točke gdje krivulja siječe negativni dio realne osi od točke (-1, 0). A fazno se može očitati kao kut između negativnog dijela realne osi i točke gdje krivulja siječe jediničnu kružnicu.
   Iz Bodeovog dijagrama amplitudno osiguranje može se očitati tako da pronađemo ω_π (frekvenciju gdje fazna karakteristika siječe -180^o) i očitamo koliko je amplitudna karakteristika na toj frekvenciji udaljena od 0dB. A fazna se može očitati tako da nađemo ω_c te očitamo koliko je fazna karakteristika na njoj udaljena od -180^o.
8. Krivulja mjesta korijena (KMK) - što predstavlja, kako se crta, čemu služi, primjer
   Krivulja mjesta korijena predstavlja kako se polovi zatvorenog regulacijskog kruga mijenjaju kako se mijenja nešto (najčešće pojačanje P-regulatora) u otvorenom regulacijskom krugu.
   Postoji niz pravila o tome kako se crta:
   1. Krivulja mjesta korijena simetrična je u odnosu na realnu os. To je zato što su korijeni polinoma s realnim koeficijentima ili realni ili se nalaze u konjugirano-kompleksnim parovima.
   2. Polovi i nule otvorenog regulacijskog kruga jednim se imenom zovu singularnosti. Točka na realnoj osi pripada krivulji mjesta korijena ako se desno od nje nalazi neparan broj singularnosti.
   3. Krivulja mjesta korijena ima onoliko grana koliko otvoreni regulacijski krug ima polova. Te grane počinju u polovima, a onoliko njih koliko ima nula završava u nulama. Preostale grane idu u beskonačnost prema asimptotama.
   4. Broj asimptota jednak je razlici broja polova i broja nula (a realni sustav uvijek ima barem toliko polova koliko ima nula).
   5. Asimptote se sijeku u točki na realnoj osi (σ, 0), gdje je \[ \sigma=\frac{\sum polovi - \sum nule}{n-m} \] Gdje je n broj polova, a m broj nula. Za realne sustave, možemo zanemariti imaginarne dijelove i samo zbrajati i oduzimati realne dijelove, jer se u realnim sustavima kompleksne singularnosti nalaze u konjugirano kompleksnim parovima, pa će se imaginarni dijelovi poništiti.
   6. Asimptote se nalaze pod kutevima u odnosu na realnu os: \[ \theta_i=\frac{180^\circ\pm k \cdot 360^\circ}{n-m}, k=0, 1 ... (n-m-1) \]
   7. Ako se krivulja mjesta korijena nalazi između dva pola na realnoj osi, tada grane iz ta dva pola idu jedna prema drugoj do točke grananja, a u toj točki grananja razilaze se pod kutem od 90^o. Analogno, ako se krivulja mjesta korijena nalazi između dvije nule na realnoj osi, postoji točka sjedinjenja u koju grane ulaze po kutem od 90^o. A te točke grananja i točke sjedinjenja realna su rješenja ove jednadžbe: \[ \sum\frac{1}{s-pol}=\sum\frac{1}{s-nula} \]
   8. Kutovi pod kojima grane krivulje mjesta korijena ulaze u nule ili izlaze iz polova dani su sljedećim formulama: \[ \theta_{izlazak}=\frac{\angle[G(s)(s-pol)^r]_{s=pol}+(2k+1)\cdot180^\circ}{r}, k=0, 1 ... (r-1) \] \[ \theta_{ulazak}=\frac{-\angle\left[\frac{G(s)}{(s-nula)^r}\right]_{s=nula}+(2k+1)\cdot180^\circ}{r}, k=0, 1 ... (r-1) \] Ovdje je r višestrukost singularnosti (pola ili nule).
   9. Sjecišta krivulje mjesta korijena s imaginarnom osi mogu se naći preko Hurwitzovog ili Routhovog kriterija.
   10. Grane krivulje mjesta korijena ne smiju se sijeći.
   Evo primjer krivulje mjesta korijena:
   
   Pomoću krivulje mjesta korijena možemo sintetizirati regulatore. Osnovni princip sinteze regulatora pomoću krivulje mjesta korijena jest da se dodavanjem pola ona izoblići prema desno, a dodavanjem nule prema lijevo. Tako je možemo izobličavati dok ona ne prolazi kroz željeni par konjugirano kompleksnih polova.

Sinteza (projektiranje regulacijskog algoritma):

1. Sinteza regulatora - pojam, osnovni okviri za sintezu i ograničenja koja treba uzeti u obzir, vrste regulacije, osnovna polazišta pri sintezi, podjela metoda i postupaka sinteze
   Regulacija je jedna od tri osnovnih vrsta upravljanja. Vrste upravljanja su:
   1. Logičko upravljanje
   2. Sekvencijalno upravljanje
   3. Kontinuirano upravljanje ili regulacija
   Vrste regulacije su:
   1. Čvrsta regulacija (x_r je konstanta)
   2. Slijedna regulacija (x_r se mijenja s vremenom)
   Prema Periću (početak 8. poglavlja), osnovni zahtjevi koji se postavljaju na regulatore (sustave upravljanja) jesu:
   1. Regulacijski krug mora biti stabilan.
   2. Poremećajne veličine z(t) trebaju što manje utjecati na izlaz sustava y(t).
   3. Izlaz sustava y(t) treba što točnije i što brže slijediti vremenski promjenjivu referentnu veličinu x_r(t).
   4. Regulacijski krug treba biti što manje osjetljiv na promjene parametara.
   Dalje ne znam.
   (UPDATE: Rekao mi je profesor na konzultacijama da su osnovna polazišta pri sintezi matematički model procesa i kakvoća regulacije kakvu treba postići.)
2. Pokazatelji kakvoće regulacije - statički i dinamički pokazatelji, povezanost između dinamičkih pokazatelja kakvoće regulacije i karakterističnih veličina regulacijskog kruga, relacije f₁-f₉
   Statički pokazatelj kakvoće regulacije jest odstupanje u stacionarnom stanju \( \epsilon_\infty \).
   (UPDATE: U skripti koju mi je na e-mail poslao profesor Slišković piše da su statički pokazatelji kakvoće regulacije: položajna pogreška, brzinska pogreška i pogreška ubrzanja.)
   Dinamički pokazatelji kakvoće regulacije su maksimalno nadvišenje σ_m, ulazno vrijeme t_u, vrijeme podizanja t_a, vrijeme prvog maksimuma t_m i vrijeme ustaljivanja t_ε (gdje je ε najčešće ili 2% ili 5%).
   
   (σ_m ili PO, percent overshoot, jednak je \( 100\frac{\Delta h}{k_s} \) ).
   Za sustave drugog reda vrijedi relacija:
   
   Dakle, što je ζ veći, to je σ_m manji. I to je relacija f₁. Ona vrijedi egzaktno za sustave drugog reda, a vrijedi približno za sustave višeg reda s jednim dominantnim parom konjugirano-kompleksnih polova.
   Relacija f₂ povezuje umnožak ω_nt_a,50 s ζ. Nadam se da profesor ne traži da tu kompliciranu formulu za tu funkciju znamo napamet. U biti, za ζ=0, umnožak ω_nt_a,50 je nešto malo više od 1, a za ζ=1, taj umnožak je približno 3, i raste otprilike linearno.
   Relacija f₃ povezuje umnožak ω_nt_3% sa ζ-om. Približno vrijedi: \[ t_{3\%}\approx\frac{4.6}{\zeta\omega_n} \] Funkcija f₄ povezuje količnik \( \frac{\omega_b}{\omega_n} \) sa ζ-om, gdje je ω_b širina pojasa, to jest, frekvencija na kojoj magnituda iznosi 70.7% magnitude na frekvenciji 0.
   Funkcija f₅ povezuje fazno kašnjenje na frekvenciji širine pojasa φ_b sa ζ-om.
   Funkcija f₆ jednaka je umnošku f₂ i f₄, i ona povezuje umnožak ω_bt_a,50 sa ζ-om.
   Funkcija f₇ povezuje količnik \( \frac{\omega_c}{\omega_n} \) s ζ-om.
   Funkcija f₈ jednaka je umnošku funkcija f₂ i f₇, i ona povezuje umnožak \( \omega_ct_{a,50} \) sa ζ-om. Približno vrijedi: \[ \omega_ct_{a,50}\approx 1.5 - \frac{\sigma_m}{250}, 0 < \zeta < 1 \] Funkcija f₉ povezuje γ sa ζ. Mada mi stvarno nije jasno kako γ može ovisiti samo o ζ-i, a ne i o K-u. Po osnovnom zdravom razumu, γ bi trebala biti manja što je K veći, zar ne? Pitat ću profesora o tome na konzultacijama. (UPDATE: Rekao mi je profesor na konzultacijama da će mi poslati skriptu koja to objašnjava.)
   Vrijedi i približna relacija: \[ \gamma [^\circ] \approx 70 - \sigma_m [\%], 0.3 < \zeta < 0.8 \]
3. Grafo-analitičke metode za sintezu regulatora - osnovna svojstva ovih metoda, postupak projektiranja regulatora grafo-analitičkim metodama
   Pojma nemam. Pretpostavljam da se pod "grafo-analitičke metode" misli na sintezu regulatora pomoću Bodeovog dijagrama ili pomoću krivulje mjesta korijena.
   UPDATE: Evo što mi je profesor rekao na konzultacijama...
   Grafo-analitičke metode su iterativne i provode u dosta koraka, pri čemu se modificiraju karakteristike kako bi se dovele u oblik koji jamči da će zatvoreni krug imati zadano vladanje.
   Među tim iteracijama mogu se prepoznati pet osnovnih koraka:
   1. Nacrtati graf prema zadanom modelu procesa.
   2. Odrediti značajke regulacijskog kruga koje treba postići (iz zadanih pokazatelja kakvoće regulacije pomoću f₁-f₉).
   3. Usporedba s polaznom situacijom (prvi korak) i s onim što se treba dobiti (drugi korak).
   4. Problem pokušati riješiti P-regulatorom (najjednostavniji i najjeftiniji regulator).
   5. Ako se problem ne može riješiti P-regulatorom, tada se regulatoru dodaju dinamički članovi (polovi i(li) nule).
   UPDATE: Kao da se sjećam da sam negdje pročitao da je prednost sinteze regulatora pomoću krivulje mjesta korijena naspram sinteze regulatora pomoću Bodeovog dijagrama (lead i lag članova) je to što se krivulja mjesta korijena može koristiti i za neminimalnofazne sustave (čije su neke nule u desno od imaginarne osi), dok se sinteza regulatora pomoću Bodeovog dijagrama može koristiti samo za minimalnofazne sustave. Međutim, nisam siguran gdje sam to pročitao i nema mi to baš previše smisla (s obzirom na to da Bodeovi dijagrami neminimalnofaznih sustava postoje, Octave ih može nacrtati). Otvorio sam pitanje o tome na nekoliko internetskih foruma (na StackExchangeu, Redditu, Discord serveru o inženjerstvu i forum.hr-u).
4. Sinteza u frekvencijskom području uz korištenje Bodeovog dijagrama - odabir pojačanja regulatora, dodavanje polova i nula regulatoru s ciljem postizanja željenog vladanja regulacijskog kruga (LEAD i LAG kompenzacija), primjer
   O LEAD-u i LAG-u, pogledajte pitanje 1.8. Ostalo ne znam.
5. Sinteza u s-području uz korištenje krivulje mjesta korijena - odabir pojačanja regulatora, utjecaj dodavanja polova i nula na oblik krivulje mjesta korijena, primjer
   O utjecaju dodavanja polova i nula na oblik krivulje mjesta korijena, vidi na kraj pitanja 2.8. Pojačanje regulatora odabiremo tako da odaberemo točku s na krivulji mjesta korijena gdje želimo da bude pol, i zatim primijenimo formulu: \[ k=\frac{\prod |s-pol|}{\prod |s-nula|} \] Ukoliko sustav nema nulā, umjesto umnoška u nazivniku stavimo jedinicu.
6. Analitičke metode za sintezu regulatora - osnovna svojstva ovih metoda, postupak projektiranja regulatora analitičkim metodama, zadavanje modelske funkcije i ograničenja u ovom smislu, standardni oblici karakterističnog polinoma
   Da bismo primijenili analitičke metode sinteze regulatora, moramo točno znati prijenosnu funkciju procesa, te trebamo imati veoma dobru predodžbu što želimo postići (modelska funkcija). Modelska funkcija je željeno vladanje zatvorenog regulacijskog kruga. Postoje ograničenja u pogledu polnog viška (razlika između broja polova i nula): polni višak modelske funkcije mora biti veći ili jednak polnom višku samog procesa, jer se regulator mora moći fizički realizirati (a regulatori s više nula nego polova ne mogu se realizirati). Postoje neki standardni oblici nazivnika modelske funkcije, recimo, često se koristi binomni oblik ili takozvani Butterworthov oblik.
7. Sinteza metodom postavljanja polova (poleplacement)
   Vidi ovu sliku:
   
   Metodi postavljanja polova zadajemo polinome prijenosne funkcije procesa B(s) i A(s), gdje je A(s) monični polinom (koeficijent uz najveću potenciju je jednak jedinici), te željeni nazivnik zatvorenog regulacijskog kruga P(s). Metoda postavljanja polova kao rezultat daje polinome R(s), S(s) i T(s), gdje je \( \frac{T(s)}{R(s)} \) prijenosna funkcija prefiltra, a \( \frac{S(s)}{R(s)} \) prijenosna funkcija regulatora. R(s) je također moničan polinom. Trebamo riješiti diofantsku jednadžbu: \[ A(s)R(s) + B(s)S(s) = P(s) \]
8. Podešavanje regulatora prema tehničkom optimumu - kriteriji za određivanje parametara regulatora, primjer
   Tehnički optimum primjenjujemo kad se proces sastoji od kaskade PT₁ članova (\( \frac{K}{1+Ts} \)), gdje je jedan T daleko veći od zbroja ostalih. Označimo taj najveći T sa T₁. Vrijedi aproksimacija: \[ \frac{K}{1+T_1s}\cdot\frac{1}{1+T_2s}\cdot\frac{1}{1+T_3s}\cdot ... \frac{1}{1+T_ns} \approx \frac{K}{1+T_1s}\cdot\frac{1}{1+T_\Sigma s}, T_\Sigma=T_2+T_3+ ... +T_n \] Tada koristimo PI-regulator, te nulom PI-regulatora poništavamo dominantni pol procesa (\( T_I=T_1 \)). Prijenosna funkcija zatvorenog regulacijskog kruga tada iznosi: \[ G_x(s)=\frac{K_O}{K_O+T_is+T_iT_\Sigma s^2} \] Tada odabiremo \( \zeta=\frac{\sqrt{2}}{2} \) te izračunamo K_O. Tako dobijemo sustav s maksimalnim nadvišenjem od 4.3% (što je u većini slučajeva prihvatljivo), ulaznim vremenom 4.7T_Σ i vremenom ustaljivanja 8.4T_Σ.
   UPDATE: Evo što piše u skripti koju mi je profesor Slišković poslao...
   Tehnički optimum temelji se na dva zahtijeva u frekvencijskoj domeni:
   1. ω_b mora biti što veći, da se smanji t_a,50.
   2. M_r (rezonantno uzdizanje) ne smije postojati, jer rezonantno uzdizanje znači da postoji σ_m.
   U praksi se dopušta maksimalno nadvišenje do 5%.
9. Podešavanje regulatora prema simetričnom optimumu - kriteriji za određivanje parametara regulatora, primjer
   Simetrični optimum primjenjuje se ili kad proces ima integralno djelovanje ili kad ima PT₁ djelovanje kad je T daleko veće od 1. Primjenjujemo PI-regulator. Ciljamo da \( \omega_c=\frac{1}{\sqrt{T_IT_\Sigma}} \) (inverz geometrijske sredine T_I i T_Σ), gdje je T_Σ zbroj svih vremenskih konstanti u procesu. Tako dobivamo brz sustav, ali s velikim nadvišenjem. Da bismo smanjili nadvišenje, ugrađujemo prefilter.
   UPDATE: Evo što piše u skripti koju mi je poslao profesor Slišković...
   Kad postoji astatizam (štogod to značilo) drugog reda, tada je čitava fazno-frekvencijska karakteristika ispod -180°. A to znači da sustav nije stabilan. Zato mu se dodaju nule, da bi se napravio interval frekvencija za koji je φ veći od -180°. I onda se cilja na to da se ω_c bude točno frekvencija na kojoj je φ na vrhu, dakle, da γ bude najveći mogući.
10. Empirijski postupci za podešavanje regulatora - polazišta za sintezu i svojstva ovih načina projektiranja regulatora, primjer (ZN-postupak, varijanta 1 i 2).
    Za empirijske postupke podešavanja regulatora ne moramo nužno znati prijenosnu funkciju procesa. Ziegler-Nichols zajednički je naziv za dvije metode podešavanja PID-regulatora. Obje pretpostavljaju da se proces može aproksimirati kao PT₂ sustav (što je istina za većinu industrijskih procesa).
    Prva metoda ide ovako (metoda ruba stabilnosti):
    1. Postavimo derivacijsko djelovanje regulatora i integralno djelovanje regulatora na nulu.
    2. Postupno pojačavamo P-djelovanje dok u jednom trenutku ne dobijemo konstantne oscilacije. Zapišemo koliko je to pojačanje pri kojem se to događa.
    3. Izmjerimo vrijeme između dvije oscilacije.
    4. Uvrstimo to vrijeme i zapisano pojačanje u tablicu, i tako dobijemo na koliko trebamo postaviti T_I, T_D i K regulatora.
    Prednost te metoda je što je jednostavna i precizna, a nedostatak je što ju je često opasno ili nemoguće provesti (dovesti sustav na rub stabilnosti).
    Druga metoda, poznata kao i metoda točke infleksije, je:
    1. Narinemo na sustav step-pobudu i mjerimo odziv.
    2. Odredimo točku infleksije odziva na step-pobudu.
    3. Na temelju te točke infleksije odredimo vrijeme zadržavanja t_z (vrijeme dok odziv ne dostigne 10% svoje konačne vrijednosti), vrijeme porasta t_a i pojačanje sustava k_s.
    4. Uvrstimo te vrijednosti u tablicu i tako dobijemo potrebno pojačanje K te vremenske konstante T_D i T_I.
    Nedostatak te metode je što je neprecizna, jer je određivanje točke infleksije problematično.