Ime
rijeke „Karašica”
Autor:
Teo Samaržija
Sažetak:
Ovo
je tekst o ideji na koju vjerujem da je svatko tko je proučavao
hrvatske toponime barem jednom naišao, naime, da je to k-r u
nazivima rijeka značilo jednostavno teći.
Pomoću kolizijske entropije i Monte Carlo numeričkih kalkulacija
vezanih za Paradoks rođendana procijenjuje se da je vjerojatnost da
se taj uzorak da su prva dva suglasnika u nazivima rijeka upravo k
i r
pojavi slučajno negdje između 1/300 i 1/17. Antičko ime za rijeku
Karašicu rekonstruira se kao *Kurrurrissia
ili *Kurrirrissia,
te se pripisuje ilirskome jeziku, da dolazi od indoeuropskog korijena
*kjers,
kao i latinska riječ za trčati,
currere.
Daju se argumenti da je ilirski jezik, za razliku od onog što se
obično pretpostavlja, pripadao centum
grupi indoeuropskih jezika. U slučaju da postoji bilo kakva zabuna,
ja ne
zastupam fonosemantičke hipoteze.
Općenito
o imenu Karašica
“Karašica”
je ime dviju rijeka u Hrvatskoj, relativno blizu jedna drugoj. Jedna
od njih se ulijeva u Dravu kod Josipovca kod Osijeka, a jedna od njih
ulijeva se u Dunav kod Batine. Stari tok dunavske Karašice
predstavlja granicu hrvatske Baranje i mađarske Baranje. Najstarija
potvrda imena Karašica
potječe iz 13. stoljeća i glasi „Karassou”.
Često
citirane etimologije
Ime
„Karašica”
ne da se objasniti hrvatskim jezikom. Za to se ime obično citiraju
dvije etimologije.
Prva
je da je to ime povezano s Carassius,
latinskim nazivom za zlatnu ribicu (ihtionimom, podrijetlom
vjerojatno iz egipatskog jezika, od istog korijena kao i grčki
ihtionim κορακινος,
koji je označavao neku ribu u rijeci Nil, mada je isto tako moguće
i da je indoeuropskog podrijetla jer sličan naziv ribe postoji i u
sanskrtu). Ta je etimologija problematična i iz fonoloških i
semantičkih razloga: tamo zlatnih ribica nema, i teško je zamislivo
da ih je u brzoj dravskoj Karašici ikada bilo
(protuargument bi mogla biti tvrdnja da je carassius
u antici možda
označavalo neku drugu ribu),
a i to posuđivanje imena Karašica
iz kasnolatinskog u hrvatski moralo bi se dogoditi nakon prelaska
kratkog a
u o
u hrvatskom jeziku (Parentium
– Poreč,
Salona
– Solin,
Tragurion
– Trogir,
Basuntius
– Bosut,
Flanona
– Plomin,
Narona
– Norin,
Bathinus
- Bosna...),
a teško da bi se hidronim posudio tako kasno.
Druga
često citirana etimologija jest da ime „Karašica”
dolazi od staroturskog „kara
sub”,
što znači „crna
voda”.
Opet, ta je etimologija problematična i zbog semantike i zbog
fonologije: nejasno je kako bi „sub”
prešlo
u 'š'
u hrvatskom jeziku,
a i opis „crna
voda”,
makar odgovarao dravskoj Karašici, definitivno ne odgovara
zapanjujuće bistroj i pjeskovitoj dunavskoj Karašici (iako bi se
pobornik te etimologije mogao izvlačiti tvrdnjom da je crn
ovdje trebalo značiti sjeverna
granica,
kao što su Grci zvali Crno more crnim jer je za njih bilo sjeverno,
ili kao što Talijani sjever zovu mezzanotte,
ponoć,
jer je sunce u ponoć, ako smo na sjevernoj polutci, sjeverno od nas,
ali je ispod horizonta).
Ime
dunavske Karašice spominje se u dokumentu iz 13.
stoljeću
kao „Karassou”
(dakle,
slavenski sufiks
-ica
dodan je naknadno) uz napomenu da se ta rijeka prije nazivala
„Mogyoros”
(možda
loše transkribirana slavenska riječ „močvara”).
Mislim
da se toj informaciji, da se dunavska Karašica prije zvala nešto
kao „Mogyoros”,
može uvjerljivo proturječiti. Današnjom
se povijesnom lingvistikom može
uvjerljivo proturječiti Konstantinu Porfirogenitu da se „Ragusa”
(današnji Dubrovnik) prije zvala „Lausa”,
a također se može proturječiti antičkim grčkim povjesničarima,
među njima i Strabonu, u 5. poglavlju 8. svitka Geografije, da se
otok Lezbos prije zvao „Issa”
i da odatle dolazi naziv naselja na tom otoku „Antissa”,
a mislim da se povijesnom lingvistikom spojenom s teorijom
informacija može proturječiti i tvrdnji da ime Karašica
nije antičko.
Rijetko
citirane etimologije
Povremeno
se u literaturi spominje etimologija da bi „kar”
u Karašica
mogao biti ilirski korijen sa značenjem teći
(ili barem neki prefiks koji je iz nekog razloga bio čest u nazivima
rijeka), koji se nalazi i u nazivima rijeka Krka,
Korana,
Krbavica,
Krapina
i Kravarščica.
Potok koji teče oko dvorca Jelengrad u Petrijevcima također se na
nekim starim kartama zove Kravica.
Uz moguću iznimku imena
Kravarščica
i Kravica
(rijeka
nazvana po životinji kravi?), ni ta se imena ne mogu objasniti
hrvatskim jezikom.
Napomena:
Recenzenti Valpovačkog godišnjaka natjerali su me da eksciziram
iduća tri odlomka, u kojima spekuliram kako se dogodilo to da nitko
prije mene nije pokušao izračunati kolika je ta slučajnost.
Pretpostavljam
da većina lingvista tu etimologiju odbacuje jer su upoznati s
paradoksom rođendana pa pretpostavljaju da se on ovdje događa i da
je velika vjerojatnost da se takav uzorak dogodi slučajno. Ja mislim
da nije tako, i da sam dokazao da je vjerojatnost da se taj uzorak
dogodi slučajno negdje između 1/300 i 1/17, a vjerojatno bliže
1/300. Malo
znanja statistike gore je nego nimalo.
A
pretpostavljam da je drugi razlog to što mnogi lingvisti misle da je
etimologija svakog toponima strogo individualni problem i da se do
nje ne može doći statističkim proučavanjem sličnih toponima. Na
što bih ja odgovorio sa: „Ako
je statistika ispala toliko korisna u medicini, zašto je ne bismo
pokušali upotrijebiti ovdje?”.
Moramo uzeti u obzir da su tadašnji
doktori takvim argumentima odgovarali Semmelweisu, da je svaki
pacijent individua i da od statistike u medicini nema koristi. I dok
su liječnici tako razmišljali, medicina je često bila
kontraproduktivna (Američkog predsjednika Georgea Washingtona
tadašnja je medicina vjerojatno ubila.).
Uzmimo u obzir i da su tadašnji biolozi tako odgovarali Mendelu.
Primjerice, Darwin je za Mendelov rad rekao: „Mathematics
in biology was like a scalpel in a carpenter's shop – there was no
use for it.”.
Isto je tako Ernest Rutherford poricao ono što su danas osnove
nuklearne fizike retorikom: „If
your experiment needs statistics, you ought to have done a better
experiment.”.
Povijest znanosti nas uči da ako pokušate primijeniti statistiku
tamo gdje se ona obično ne primjenjuje, naletjet ćete na hrpu
besmislenih argumenata protiv uporabe statistike, i vaš će rad biti
proglašen neznanstvenim. Meni se čini da znanstvenici koji se danas
bave nazivima mjesta u Hrvatskoj čine upravo istu pogrešku koju su
činili liječnici kada su odbacivali Semmelweisov rad ili biolozi
kada su odbacivali Mendelov rad ili Rutherford kad je odbacivao ono
što su danas osnove nuklearne fizike. Naučimo lekciju iz povijesti
znanosti i nemojmo činiti tu istu grešku opet! Prihvatimo da, ako
ćemo se baviti empirijskim stvarima, moramo barem ponekad
upotrijebiti statistiku!
Pretpostavljam
da je treći razlog zašto lingvisti odbacuju tu etimologiju
pouzdanje u tradicionalne metode proučavanja toponima. Tradicionalna
metoda proučavanja toponima bazira se na pretpostavci da su
etimologije iz jezika koje dobro poznajemo vjerojatnije od
etimologija iz jezika koje ne poznajemo. Ne vidim na čemu se ta
pretpostavka bazira.
U
biti, taj se uzorak da se to k-r ponavlja u hrvatskim nazivima rijeka
odbacuje kao slučajnost, ali (koliko ja znam) nitko nije ni pokušao
izračunati kolika bi to slučajnost morala biti.
To je, po meni, krajnje neznanstveno, jer su p-vrijednosti osnova
današnje
znanstvene metode, i to s razlogom.
Do
sada je glavni argument za
tu etimologiju bio nešto kao: „Karašice
izgledaju različito (jedna je mutna, druga bistra, jedna je brza,
druga spora...) i imaju različit biljni i životinjski svijet. I ta
je razlika u donjim tokovima bila još veća prije kopanja Gatskog
kanala. Nema očitog razloga zašto bi Karašice nosile isto ime,
osim ako ne pretpostavimo da je Karašica značilo nešto kao
'tekućica' ili 'voda koja teče'.”.
Ali mislim da se primjenom osnova teorije informacija može dati još
bolji argument za tu etimologiju.
Paradoks
rođendana
Paradoks
rođendana je da je ljudima teško intuitivno razumjeti razliku
između brzine rasta permutacijske funkcije i brzine rasta
eksponencijalne funkcije. Većinu će ljudi iznenaditi to što, ako
imamo skupinu od 23 čovjeka, vjerojatnost da će dvoje od njih imati
isti rođendan iznosi preko 50%. Tu je vjerojatnost relativno lagano
analitički izračunati. Pretpostavimo, radi jednostavnosti, da
godina ima 365 dana, i da je svaki od njih podjednako vjerojatan da
bude rođendan (u stvari, postoje prijestupne godine, te se više
djece rađa u proljeće nego u drugim godišnjim dobima, ali
zanemarimo sad te stvari). Broj mogućih rasporeda rođendana u 23
osobe da nitko ne dijeli isti rođendan iznosi 365!/(365-23)!, gdje
uskličnik označava faktorijel, to jest, umnožak prvih n
prirodnih brojeva. Za prvu osobu ima 365 mogućih rođendana, za
drugu 364, za treću 363, i tako dalje, dok za 23. osobu ima
356-23+1=343 mogućnosti, dakle, ukupno je to
365*364*363*...*343=365!/(365-23)!. To se zove permutacijska
funkcija, i često se označava kao funkcija s dva argumenta P(n,m).
Broj mogućih rasporeda rođendana pri kojima te dvadeset i tri osobe
mogu dijeliti rođendane iznosi, naravno, 365^23, i to se zove
eksponencijalna funkcija. Dakle, vjerojatnost da nitko od te 23 osobe
ne dijeli rođendan iznosi (365!/(365-23)!)/(365^23), što je nešto
manje od 50%. No, nema očitog načina da se analitički izračuna
vjerojatnost da se dogodi da troje od te 23 osobe dijele isti
rođendan, što je slično ovome problemu.
Numerički
izračuni paradoska rođendana
Međutim,
to se može izračunati numerički jednostavnim računalnim
programom,
recimo, ovim programom pisanim u programskom jeziku JavaScript:
1
let
iznad_koliko_kolizija_brojimo = 2,
2 koliko_ima_ljudi = 23,
3 koliko_smo_puta_dobili_toliko_kolizija = 0,
4 koliko_smo_puta_izvrtili_simulaciju = 100_000;
5 for (let brojac = 0; brojac < koliko_smo_puta_izvrtili_simulaciju; brojac++) {
6 let koliko_ljudi_ima_rodendan_na_taj_dan = [];
7 for (let brojac = 0; brojac < 365; brojac++)
8 koliko_ljudi_ima_rodendan_na_taj_dan.push(0);
9 for (let brojac = 0; brojac < koliko_ima_ljudi; brojac++)
10 koliko_ljudi_ima_rodendan_na_taj_dan[Math.floor(Math.random() * 365)] += 1;
11 let jesmo_li_nasli_potreban_broj_kolizija = false;
12 for (let brojac = 0; brojac < 365; brojac++)
13 if (
14 koliko_ljudi_ima_rodendan_na_taj_dan[brojac] >=
15 iznad_koliko_kolizija_brojimo
16 ) {
17 jesmo_li_nasli_potreban_broj_kolizija = true;
18 break;
19 }
20 if (jesmo_li_nasli_potreban_broj_kolizija)
21 koliko_smo_puta_dobili_toliko_kolizija += 1;
22 }
23 console.log(
24 `Vjerojatnost da ${iznad_koliko_kolizija_brojimo} od ${koliko_ima_ljudi} dijeli isti rodendan iznosi ${
25 (koliko_smo_puta_dobili_toliko_kolizija /
26 koliko_smo_puta_izvrtili_simulaciju) *
27 100
28 }%.`
29 );
Vjerojatnost da barem 3 osobe od 23 osobe dijele isti rođendan iznosi 1.26%.
A vjerojatnost da barem 4 osobe od 23 osobe dijele isti rođendan iznosi 0.018%.
Očito, paradoks rođendana veoma brzo nestaje kako se broj osoba koje bi trebale dijeliti isti rođendan povećava.
Štoviše, ako pretpostavimo da hrvatski jezik ima 20*20=400 parova suglasnika koji se s podjednakom vjerojatnosti pojavljuju na početku riječi, vjerojatnost da 6 od 100 rijeka slučajno počinje s istim parom suglasnika iznosi 1/10'000.
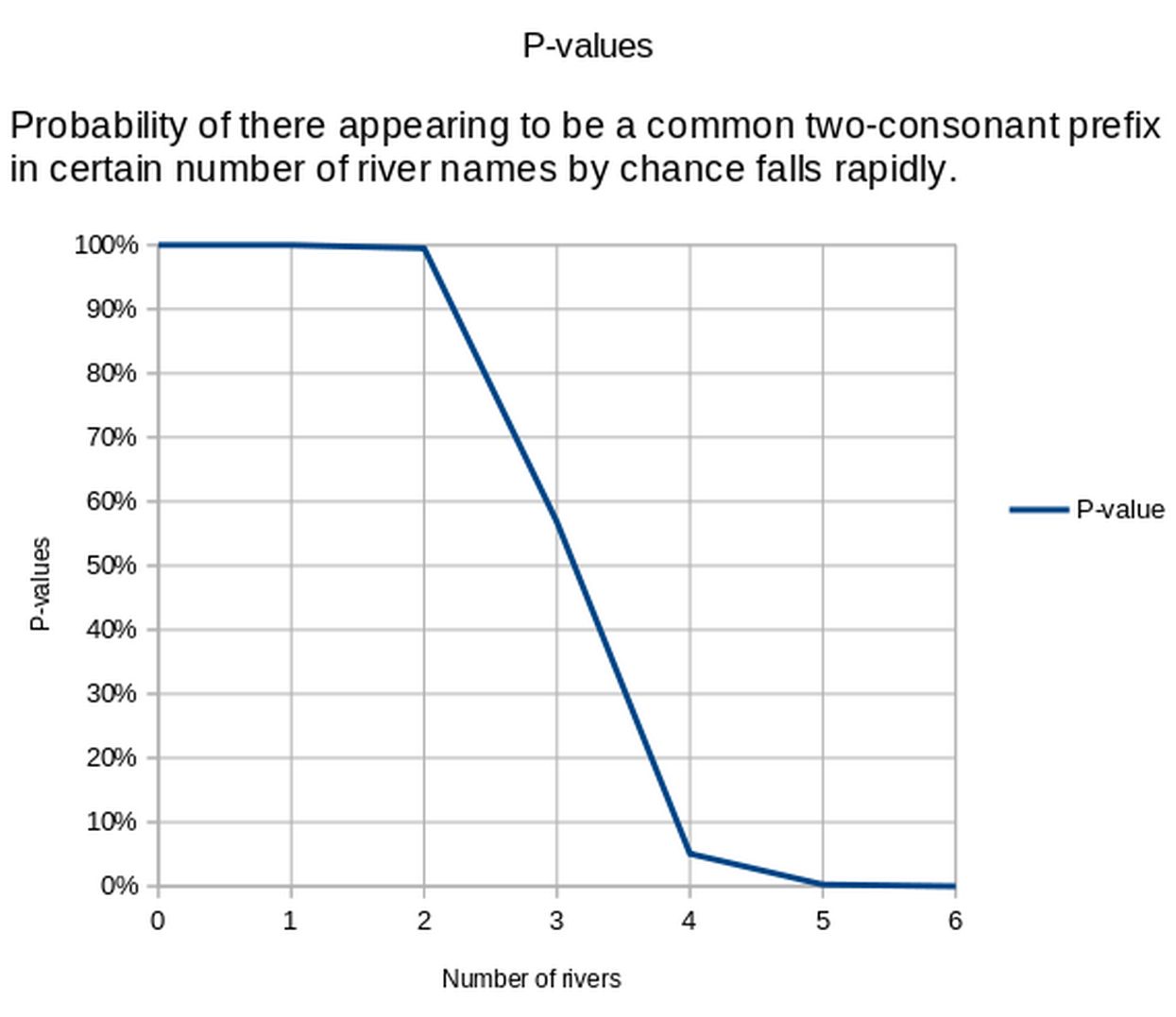
No, koliko je ta pretpostavka, na kojoj se taj krajnje pojednostavljeni model jezika zasniva, realistična?
Je li kolizijska entropija para suglasnika u nazivu mjesta uistinu približno log2(400) bita po simbolu?
Možemo li uistinu pretpostaviti da u hrvatskom jeziku postoji 400 parova suglasnika potencijalno odvojenih samoglasnikom od kojih su svi jednako vjerojatni?
Entropija
u informatici
Entropija
je jedno od najvažnijih pojmova u informatici. Riječ „entropija”
grčkog
je podrijetla i
znači „nered”
ili „nepredvidivost”.
Pojam se prvo pojavio u fizici, a u informatiku ga je preuzeo Claude
Shannon 1948. godine u svojoj knjizi „A
Mathematical Theory of Communication”.
U fizici se entropija mjeri u džulima po kelvinu, a u informatici u
bitovima po simbolu. Bit
(inače engleska riječ koja znači
mali dio,
od istog korijena kao njemački bisschen)
je
mjerna jedinica informacije, to je onoliko informacije koliko nosi
jedna binarna znamenka, koja može biti ili nula ili jedinica.
Shannonova
entropija
Shannonova
entropija nekog stringa mjeri se kao zbroj umnožaka relativnih
frekvencija pojedinih simbola u tom stringu i njihovih logaritama
pomnožen s -1. U informatici se, naravno, najčešće koristi
binarni logaritam. Recimo da imamo string „abb”.
Relativna frekvencija simbola 'a'
iznosi 1/3, a relativna frekvencija simbola 'b'
iznosi 2/3. Apsolutne frekvencije, koje ne uzimaju u obzir duljinu
stringa, naravno, iznose 1 i 2. Shannonova entropija tog stringa
iznosi ((1/3)*log2(1/3)+(2/3)*log2(2/3))*(-1)=0.9182
bita po simbolu. Shannonova entropija je donja granica, i obično
izvrsna aproksimacija, koliko će string biti dugačak ako se sažme
jednim jednostavnim, ali često korištenim, algoritmom sažimanja
stringova, koji se zove Huffmanovo kodiranje (poznato i pod nazivom
kodiranje
minimalnim težinskim stablom).
Demonstraciju toga imate na mojoj web-stranici.
Nasumični stringovi, bez značenja, imaju visoku entropiju, i ne
mogu se sažeti. Šifrirani stringovi, ako je šifra dobra, isto tako
imaju visoku entropiju. Slabe šifre kao što su zamjena slovo za
slovo entropiju mijenjaju malo ili nimalo, ali dobri algoritmi
šifriranja stvaraju stringove koji se mjerenjem entropije ne mogu
razlikovati od nasumičnih stringova. Digitalni slika i zvuk imaju
entropiju veću od teksta, ali manju od nasumičnih ili dobro
šifriranih stringova. Shannonova entropija analogna je
Boltzmanovoj entropiji
u termodinamici, gdje je
Boltzmanova entropija
čestice integral od umnoška vjerojatnosti da se neka čestica
nalazi na nekoj lokaciji i logaritma te vjerojatnosti.
Kolizijska
entropija
Kolizijska
entropija je sličan pojam. On se računa kao negativni logaritam
vjerojatnosti da, ako dva puta nasumično odaberemo simbol iz
stringa, oba puta odaberemo jednaki. Za string „abb”
on bi se mogao ovako izračunati. Ako prvi puta odaberemo znak 'a',
vjerojatnost da ćemo drugi put odabrati isti znak iznosi 1/3. Ako
prvi puta odaberemo znak 'b', vjerojatnost da ćemo drugi put
odabrati isti znak iznosi 2/3. Dakle, ukupna vjerojatnost kolizije
(pojave da dva puta odaberemo isti znak) iznosi 1/3*1/3+2/3*2/3=5/9.
Dakle, kolizijska entropija tog stringa iznosi -log2(5/9)=0.8479
bita po simbolu. Mislim da je očito da je kolizijska entropija
upravo ono što nama treba da izračunamo kolika je vjerojatnost da
se taj uzorak da imena rijeka u Hrvatskoj počinju s
k+(samoglasnik+)r pojavi slučajno.
Kolizijska entropija se često koristi u informatici kao bolja
procjena stvarne nepredvidivosti stringa nego što ga pruža
Shannonova entropija. Shannonova entropija, naime, često daje
iluziju da je string više nepredvidiv nego što uistinu jest.
Također, moderni algoritmi sažimanja koji ne sažimaju
simbol-po-simbol kao Huffmanovo kodiranje, već prepoznaju česte
nakupine simbola (na engleskom jeziku, recimo, nakon slova 'q'
gotovo uvijek slijedi slovo 'u',
pa nema smisla kodirati 'q'
i 'u'
kao posebne simbole u tom slučaju), mogu postići znatno kraći
string nego što to predviđa Shannonova entropija, pa je kolizijska
entropija nerijetko bolja procjena koliko će sažeti string biti
dugačak. Kolizijska
entropija se, kako sam doznao nakon što sam napisao prvu verziju
ovog teksta, može računati i kao negativni logaritam sume kvadrata
relativnih frekvencija (a ne samo Monte Carlo metodom, da se mnogo
puta nasumično odaberu dva simbola iz stringa i broji koliko se puta
desilo da budu jednaki).
Kolizijska
entropija ljudskih jezika
Kolizijska
entropija ljudskih jezika zapanjujuće je niska, mnogo niža nego što
je u protokolima za komunikaciju između računala. Kad sam napravio
program da izmjerim kolizijsku entropiju suglasnika u nekom tekstu i
zadao mu da izmjeri kolizijsku entropiju suglasnika u nekom tekstu na
engleskom jeziku, očekivao sam da će on ispisati rezultat nešto
manji od log2(21)
bita po simbolu, jer engleski jezik ima 21 suglasnik. Međutim, taj
program je ispisao da ona iznosi svega log2(11)
bita po simbolu. Pa na što onda odlazi sva ta entropija? S obzirom
da je taj program također ispisao da je najčešći suglasnik
(dakle, suglasnik s najmanje entropije) bio ‘t’,
pretpostavio sam da većina te entropije odlazi na sintaksu, jer
engleska gramatika često zahtijeva da se u rečenice umeću riječi
bez značenja kao što su “the”,
“it”,
“that”,
„then”
i “than”.
Da to provjerim, zadao sam tom programu da izmjeri entropiju
suglasnika u listi riječi od spell-checkera Aspella,
dakle, teksta iz kojeg je eliminarana sintaksa. Očekivao sam da će
on tada ispisati rezultati svega nešto manji od log2(21)
bita po simbolu. Međutim,
on je ispisao da je kolizijska entropija suglasnika u listi riječi
od spell-checkera svega log2(13)
bita po simbolu, te da je najčešći suglasnik 'r'
(vjerojatno zbog iznimno čestih engleskih prefiksa i sufiksa „re-”
i „-er”,
“re-”
za
glagole koji označavaju neko ponavljanje, a „-er”
za pravljenje imenica od glagola sa značenjem „onaj
koji nešto radi”).
Za hrvatski jezik entropije su bile log2(13)
bita po simbolu i log2(14)
bita po simbolu, a najčešći suglasnik je u oba slučaja bio 'n'.
Za njemački jezik entropije su bile log2(12)
bita po simbolu i log2(15)
bita po simbolu, a najčešći suglasnik je opet u oba slučaja 'n'.
Za talijanski je jezik entropija suglasnika u dugačkom tekstu bila
log2(12.5)
bita po simbolu, a najčešći suglasnik bio je 'n'.
U Aspellovom rječniku talijanskog jezika entropija je bila log2(15),
a najčešći suglasnik bio je 'r'.
Za francuski je jezik entropija suglasnika u dugačkom tekstu bila
log2(10)
bita po simbolu, a najčešći suglasnik bio je 's'.
U Aspellovom rječniku francuskog jezika entropija suglasnika bila je
log2(11)
bita po simbolu, a najčešći suglasnik isto je bio 's'.
Ime jezika
|
Kolizijska entropija
suglasnika u dugačkom tekstu
|
Najčešći suglasnik u
dugačkom tekstu
|
Kolizijska entropija
suglasnika u Aspellovoj listi riječi
|
Najčešći suglasnik u
Aspellovoj listi riječi
|
Kolizijska entropija
sintakse
|
Engleski
|
log2(11)
|
t
|
log2(13)
|
r
|
0.241
|
Njemački
|
log2(12)
|
n
|
log2(15)
|
n
|
0.322
|
Hrvatski
|
log2(13)
|
n
|
log2(14)
|
n
|
0.107
|
Talijanski
|
log2(12.5)
|
n
|
log2(15)
|
r
|
0.263
|
Francuski
|
log2(10)
|
s
|
log2(11)
|
s
|
0.138
|
Napominjem
da bi brojevi u drugom i četvrtom retku mogli biti podcjenjivanje,
jer program kojim sam to mjerio ignorira ne-ASCII znakove (č,
ć, đ, ž, š...).
Za brojeve u šestom stupcu teško je reći jesu li podcjenjivanje
ili precjenjivanje, naime, mogli bi biti i precjenjivanje jer
logaritamska funkcija brže raste što se više pomičemo prema
lijevo (za manje brojeve). Malo
mi je zapanjujuće to što je entropija sintakse njemačkog jezika,
koja iznosi log2(15)-log2(12)=0.3219
bita po simbolu, veća od entropije sintakse engleskog jezika, koja
iznosi log2(13)-log2(11)=0.241
bita po simbolu. Iako ne znam u detalje gramatiku njemačkog jezika,
iz onoga što znam, jako mi se činilo da njemački jezik ima
jednostavniju sintaksu, ali da zato ima znatno kompliciraniju
morfologiju. No, s tvrdim podacima se ne možeš svađati.
Ili, još vjerojatnije, ti se podaci mogu tumačiti da pokazuju da
kompliciranost sintakse nekog jezika i kolizijska entropija sintakse
tog istog jezika nisu u strogoj korelaciji. Dakle,
na sintaksu odlazi relativno malo entropije, pogotovo u hrvatskom
jeziku. Pa, odlazi
li onda ostatak entropije na morfologiju (da ne utječe na
vjerojatnosti u toponimiji) ili na fonologiju (da utječe na
vjerojatnosti u toponimiji)?
Mogući
prigovor – odlazi li entropija na pravopis
Korisnik
forum.hr-a
zvan Al
Dente
komentirao je da moj eksperiment da odredim koliko kolizijske
entropije odlazi na sintaksu nije dobar jer možda je stvarna
entropija engleskog jezika znatno veća, samo je engleski pravopis
skriva. Po njemu, trebao sam izmjeriti kolizijsku entropiju teksta
pisanog IPA-om (internacionalnom fonetskom abecedom), a ne
tradicionalnom latinicom. On misli da je glavni razlog zašto je e
znatno češći od drugih samoglasnika to što engleski pravopis duge
samoglasnike označava s tihim e
na kraju riječi, a da je glavni razlog zašto je th
najčešća skupina od dva slova to što th
označava dva različita fonema: zvučni dentalni frikativ i bezvučni
dentalni frikativ.
Kao
prvo, uzmimo u obzir da je Levy prigovorio Semmelweisu, između
ostalog, „A
zašto nije proveden jednostavniji i pouzdaniji eksperiment, da se
prekine sav anatomski rad?”.
Ako razumijete zašto Levyjev prigovor Semmelweisovom eksperimentu
nije na mjestu, trebali biste razumjeti i zašto Al
Denteov
prigovor na moj eksperiment nije dobar. Eksperimentima se
kontradiktira drugim eksperimentima, a ne spekulacijama. Zapravo, Al
Denteov
prigovor još je manje smislen nego Levyjev prigovor, jer je Levy
predlagao jednostavniji eksperiment, a Al
Dente
predlaže kompliciraniji eksperiment.
Ja
nemam dojam da pravopis znatno smanjuje kolizijsku entropiju
engleskog jezika. Engleski pravopis više-manje predstavlja kako se
engleski jezik govorio prije nekoliko stoljeća. Zar ćemo tvrditi da
se kolizijska entropija jezika s vremenom uvijek povećava? Za većinu
riječi u engleskom jeziku koje imaju tiho e
na kraju riječi, to se je e
prije nekoliko stoljeća stvarno izgovaralo. Kasnije je prešlo u
poluglas, pa nestalo. A glasovi koje označava th
označavaju se jednako jer su prije nekoliko stoljeća i bili isti
glas, bezvučni dentalni frikativ. Kasnije se pojavio zvučni
dentalni frikativ kao njegov alofon, i osnovno pravilo bilo je (kao i
danas) da je th
između dva samoglasnika zvučno, a inače bezvučno. Tek je daljnjim
glasovnim promjenama postao zaseban fonem. Izvorni govornici
današnjeg engleskog jezika uglavnom se iznenade kada doznaju da th
označava dva različita glasa, i ne mogu pouzdano reći je li u
nekoj riječi th
zvučan ili bezvučan (kao što ni mi ne možemo pouzdano reći je li
u nekoj riječi ije
ili
je,
ili je li u nekoj riječi naglasak uzlazan ili silazan). Jedan od
osnovnih principa povijesne lingvistike je da su jezici u povijesti
imali ista statistička svojstva kao današnji jezici. Tvrditi da su
jezici u prošlosti imali manju kolizijsku entropiju nego današnji
jezici očito kontradiktira tom principu. Iz tog razloga mislim da je
sugerirati da pravopis znatno smanjuje entropiju pisanog jezika u
najmanju ruku neosnovano.
Na
spekulacije ne moramo odgovoriti kompliciranim eksperimentima i
izračunima, već možemo i ovako, razumnim spekulacijama.
Naravno,
moguće je da sam u krivu. Moguće je da je netko napravio studiju
koja pokazuje da duboki pravopis (kakav imaju engleski, francuski
ili, vjerojatno najekstremniji primjer, tibetanski) smanjuje
entropiju pisanog jezika. Otvorio sam pitanje o tome na par
internetskih foruma
.
Razlika
između
fonologije i fonotaktike
Fonologija
je dio gramatike koji određuje koji su fonemi (glasovi koje jezik
razlikuje) dozvoljeni u jeziku i u kojim kombinacijama. U Bibliji je,
u Knjizi o sucima, u 12. poglavlju, napisano da izvorni govornici
efraimatskog jezika nisu mogli izgovoriti hebrejsku riječ
šibboleth
(ljuska oko zrna pšenice), da su je izgovarali kao
sibbolet.
Efraimatska fonologija, dakle, nije dopuštala glas š,
barem ne na početku riječi, a vjerojatno uopće. Fonotaktika je dio
fonologije koji određuje u kojim su kombinacijama fonemi (glasovi
koje jezik razlikuje) dopušteni. U japanskom jeziku, recimo, postoje
glasovi v,
j,
te samoglasnici a,
e, i, o
i u,
kao u hrvatskom jeziku. Međutim, iako slogovi ja,
jo
i ju
postoje u japanskom jeziku, slogovi ji
i je
(koji je, usput, najčešći slog u hrvatskom jeziku) ne postoje osim
u posuđenicama. Isto tako, iako slogovi va
i vo
postoje, slogovi vi,
vu
i ve
ne
postoje osim u posuđenicama. Ili, recimo, Japancima i Hrvatima lako
je izgovoriti riječ
tsunami,
dok izvornim govornicima engleskog jezika nije jer u engleskom jeziku
riječ ne može počinjati na
ts.
Ili,
recimo, Etrurcima je bilo nespretno izgovarati grčka naziva
božanstava puna samoglasnika, pa se teonim (ime božanstva) Herakles
u etrurski jezik posudio kao Herkles,
a govornicima latinskog jezika bilo je nespretno izgovoriti
suglasničku skupinu rkl,
pa su Herkles
u svoj jezik posudili kao Hercules.
Entropija
fonotaktike i što nam ona daje
Dosjetio
sam se da bih jednim krajnje jednostavnim računalnim programom mogao
izmjeriti Shannonovu entropiju parova suglasnika u nekom ljudskom
jeziku, te da bih tako lako mogao odrediti entropiju fonotaktike, a
time i procijeniti kolika bi entropija fonologije mogla biti
(ustvari, ako znate da je kolizijska entropija jednaka logaritmu
zbroja kvadrata relativnih frekvencija pomnoženim
s -1,
jednostavno je napraviti i računalni program koji računa kolizijsku
entropiju toga, ali ja tada to nisam znao). Razlika entropije
suglasnika pomnožene s 2 i entropije parova suglasnika dala bi nam
entropiju fonotaktike. S obzirom da je fonotaktika dio fonologije, to
bi nam onda dalo donju granicu koliko fonologija može oduzimati
entropije. Shannonova entropija parova suglasnika u spell-check
rječniku hrvatskog jezika, kako sam pomoću tog programa izmjerio,
iznosi log2(229)=7.839
bita po simbolu.
Napisao sam i program koji generira mnogo nasumičnih nizova znakova
od
21 različitog znaka (suglasnika engleske abecede) i dugačkih 100
znakova
te računa njihove Shannonove i kolizijske entropije, te sam na
temelju podataka koje je on ispisao matematički sumnjivim metodama
(pretpostavio sam da krivulja koja prikazuje odnos Shannonove i
kolizijske entropije ima isti oblik bez obzira na broj različitih
simbola u stringu, da s time samo mijenja veličinu) procijenio
da bi kolizijska entropija od nečega, čija Shannonova entropija
iznosi 7.839 bita po simbolu i što ima 676 različitih simbola,
iznosila 5.992 bita po simbolu.
(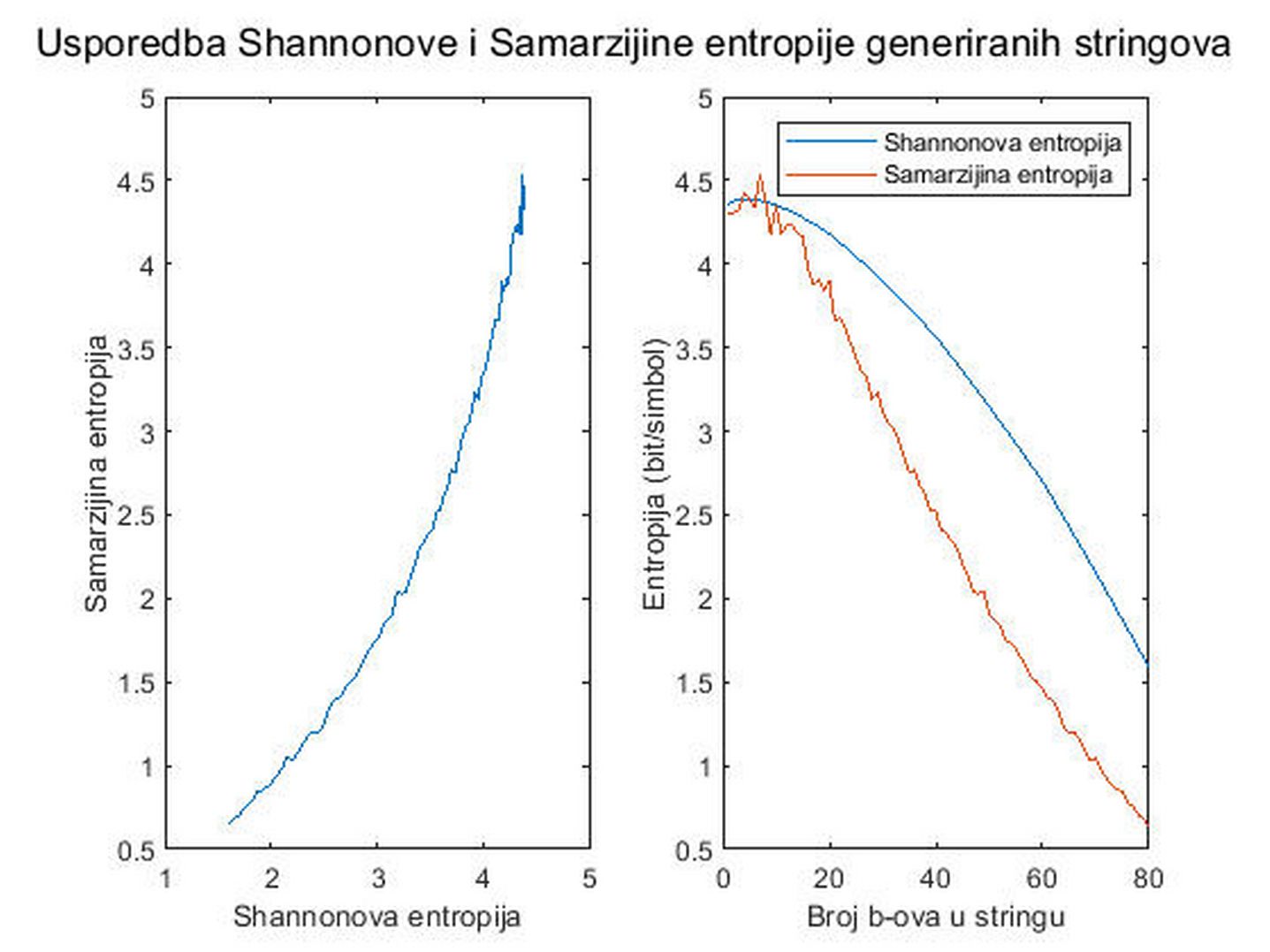
Ovdje
„Samaržijina
entropija”
znači „kolizijska
entropija”,
jer tada još nisam znao kako se ona zove, pa sam je tako nazvao. Tek
me je kasnije netko na internetskom forumu uputio da je mađarski
informatičar Alfred Renyi prije mene došao na istu ideju i nazvao
ju „kolizijska
entropija”.)
Naime,
hrvatski jezik ima 26*26=676 mogućih parova suglasnika. Tih 5.992
bita po simbolu onda bi bilo koliko entropije parova suglasnika
ostaje semantici, dakle, tih 5.992 bita po simbolu ne pripada ni
fonologiji, niti morfologiji, niti sintaksi. Bez fonotaktike,
entropija parova suglasnika bila bi dvostruko veća od entropije
pojedinih suglasnika u rječniku, dakle, za hrvatski bi jezik bila
2*log2(14)=7.615
bita po simbolu. Fonotaktika, dakle, od entropije hrvatskog jezika
oduzima 7.615-5.992=1.623 bita po simbolu. Za usporedbu, iz podataka
koje smo izmjerili možemo izračunati da sintaksa
oduzima samo 2*(log2(14)-log2(13))=0.214
bita po simbolu. Množimo s 2 jer su se mjerenja iz kojih smo dobili
13 i 14 odnose na pojedine suglasnike, a ne na parove suglasnika.
Tamo je simbol bio jedan suglasnik, sada je simbol par suglasnika.
Fonotaktika, dakle, na entropiju hrvatskog jezika ima
1.623/0.214=7.584 puta veći utjecaj nego što ima sintaksa. Koliko
onda entropije odlazi na morfologiju? Pod pomalo neopravdanom
pretpostavkom da nijedan drugi dio fonologije osim fonotaktike ne
oduzima entropiju, možemo procijeniti da na morfologiju odlazi
log2(676)-1.623-0.214-5.992=1.572
bita po simbolu, neznatno manje nego na fonotaktiku. Pod morfologijom
ovdje se podrazumijeva ne samo morfologija u tradicionalnom smislu te
riječi, već i tvorba riječi, to jest, prefiksi i sufiksi koji
postaju dio osnove pri deklinaciji i konjugaciji. Dakle, 1.572 bita
po simbolu je gornja granica koliko, po onome što smo izmjerili,
morfologija može oduzumati entropije od hrvatskog jezika, dok je
1.623 bita po simbolu donja granica koliko fonologija može oduzimati
od hrvatskog jezika.
P-vrijednost
tog k-r
uzorka u hrvatskim nazivima rijeka
Ako
pretpostavimo da je kolizijska entropija morfologije uistinu 1.572
bita po paru suglasnika, a entropija fonologije uistinu 1.623 bita po
paru suglasnika, vjerojatnost da se onaj uzorak da imena rijeka
počinju sa k+(samoglasnik+)r
pojavi slučajno iznosi, kako se može izračunati preko onog
programa vezanog za paradoks rođendana, 1/300. Ako pretpostavimo da
morfologija oduzima 0 bita po paru suglasnika, a fonologija oduzima
1.623+1.572=3.195 bita po paru suglasnika, ta vjerojatnost iznosi
1/17. A mislim da bi se svatko složio da je prva pretpostavka daleko
bliža realnosti.
Sad, možda
je pretpostavka da u Hrvatskoj ima 100 rijeka nerealistična, pa su
te p-vrijednosti podcjenjivanje. Ipak, mislim da su vjerojatno znatno
precjenjivanje, jer dva
suglasnika na početku riječi
dopuštalo bi i imena rijeka kao što je *Ikura
(sa samoglasnikom na početku, i s neočekivanim samoglasnikom između
k i r ako pretpostavimo da to dolazi od *karr~kurr),
kakva
se ne pojavljuju.
Mislim
da sam dokazao tvrdim podacima da je „kar-”
u imenu Karašica
ili korijen sa značenjem „teći”,
ili, manje vjerojatno, prefiks koji se iz nekog razloga često
dodavao hidronimima. Tvrdi podaci se za sada rijetko mogu koristiti u
toponimiji (jer lingvistika još nije dovoljno razvijena za to), ali
u ovom se slučaju mogu. Programi s kojima sam ove stvari mjerio i
računao dostupni su na mojoj web-stranici,
i detaljno su opisani u mom seminaru Fonološka
evolucija jezika.
Spekulacije
o etimologiji tog korijena k-r
i
kako se Karašica mogla zvati u antici
Mislim
da bi taj glagolski korijen za teći
u različitim dijalektima ilirskoga glasio ili karr-
ili kurr-,
u oba slučaja s kratkim samoglasnikom, te da dolazi od indoeuropske
riječi za konja, *kjers,
od koje dolazi i latinska riječ za trčati,
currere.
Alternativno,
mogli bismo tvrditi,
kako misli MechaLiver
s foruma forum.hr,
da
taj glagolski korijen nije
značio teći,
nego da je značio
rasti,
u smislu rijeka
nestalnog vodostaja,
te da dolazi od indoeuropskog korijena *kjer,
odakle i latinska riječ za rasti,
crescere.
Prema Hansu Kraheu, oko 30-ak rijeka u Europi dobilo je svoj naziv po
korijenu *h2elm
(rasti), među njima i rijeka Yealm u Engleskoj te rijeka Almar u
Španjolskoj.
Za
ablaut samoglasnika
a
i
u
usporedite toponime
Marsonia
(ilirsko ime za Slavonski Brod) i
Mursa
(ilirsko
ime za Osijek), gotovo sigurno od istog korijena. Ime
Korana
dolazi od
karr-,
a ostala imena rijeka o kojima smo raspravljali dolaze od
kurr-,
osim vjerojatno imena Krapina
(Mislim da bi Okamova britva favorizirala hipotezu da se Krapina u
antici zvala nešto kao *Karpona
i da 'a'
dolazi od metateze likvida više nego hipotezu da se zvala nešto kao
*Kurrippuppona
i
da 'a'
dolazi od poluglasa, zato što je *Karpona
lakše izgovoriti, iako bi oboje u današnji hrvatski dalo Krapina).
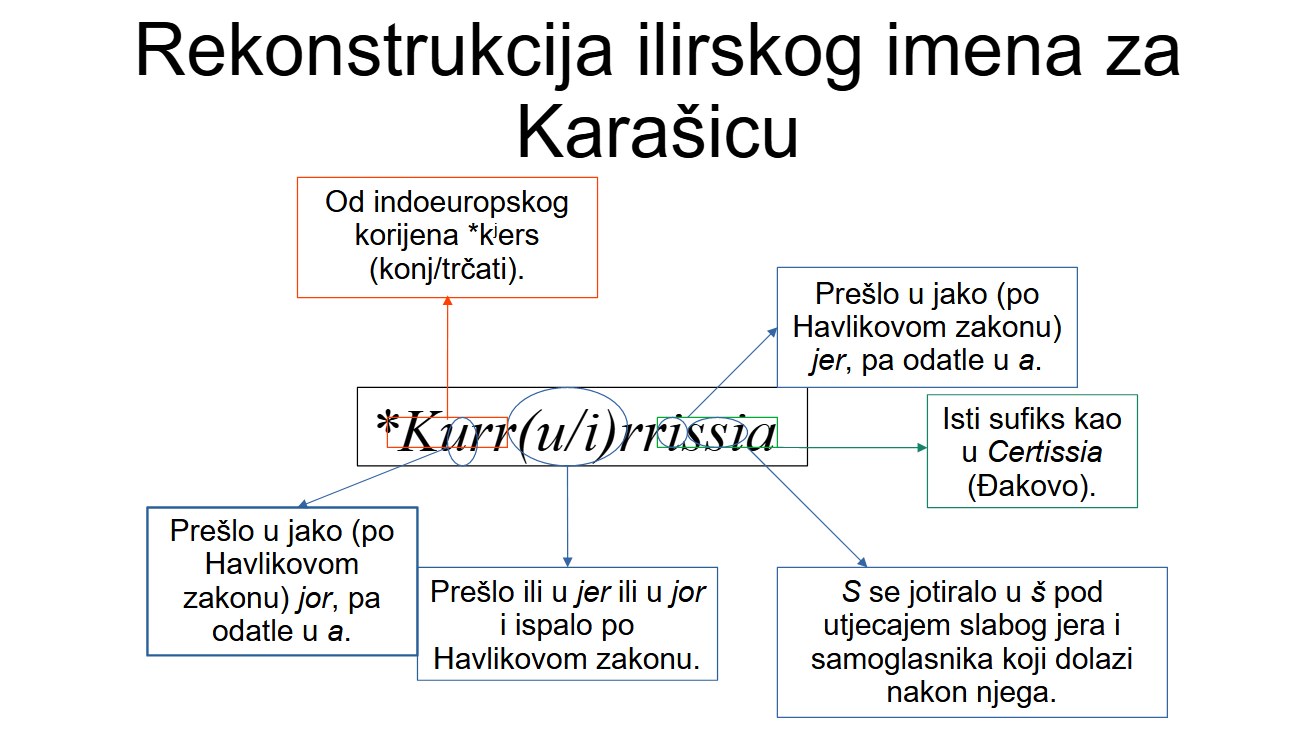
Mislim
da je ilirsko ime za rijeku Karašicu bilo
Kurr-(kratko
u
ili kratko
i)-rr-(kratko
u
ili kratko
i)-ssia,
da su ti kratki
u-ovi
i kratki
i-jevi
bili posuđeni u hrvatski jezik kao jor
ili jer,
te da je taj jer
ili jor
u drugom slogu ispao po Havlikovom zakonu, a da su ostali, naravno,
prešli u a.
Ustvari, s obzirom na to da znamo da
je u ilirskom jeziku postojao sufiks -issia,
kao u antičkom imenu za Đakovo,
Certissia
(štogod cert
značilo), i za Omiš, Almissia
(alm
je vjerojatno značilo
plodan),
a
ne znamo da je postojao sufiks -ussia,
možemo pretpostaviti da je samoglasnik u trećem slogu bio kratko
i,
a ne kratko
u,
dakle, da je antičko ime za Karašice
bilo ili
Kurrurrissia
ili
Kurrirrissia.
Napomena:
Recenzenti Valpovačkog godišnjaka natjerali su me da eksciziram
idući odlomak (ali ne i sliku), u kojem spekuliram odakle dolazi
drugi morfem od *Kurr-urr-issia
ili *Kurr-irr-issia.
Ako
je u drugom slogu bilo
u,
taj bi slog mogao dolaziti od indoeuropskog korijena *weh1r
(voda), u nultom ablautu. Indoeuropski korijen *weh1r
postojao je u ilirskom jeziku, od njega dolazi ime Varvaria,
antičko ime za Bribir kod Šibenika.
Mali problem je što je
u
u drugom slogu u
Kurrurrissia
kratko, a od nultog ablauta od *weh1r
očekivali bismo dugo
u
(zbog h1),
da daje *Kurrurissia (primijetite da r
u drugom slogu nije udvostručeno), što bi u modernom hrvatskom dalo
*Kriraša (jer bismo očekivali da se ilirsko dugo u
posudi kao jeri, koji u hrvatskom jeziku prelazi u i).
Ali od istog problema pati i Ivšićina etimologija da Varvaria
dolazi od *weh1r
(Zašto
drugi ablaut od *weh1r,
*woh1r,
ne bi u ilirskom prešao u *vor
nego u *var?).
Kao da je h1
u *weh1r
u ilirskom jeziku nestao, a da nije ostavio traga u naglasku.
Ako
je u drugom slogu bilo
i,
on bi možda mogao dolaziti od istog korijena kao
Ira,
kako je Ravenjanin zvao neku rijeku u Panoniji, vjerojatno Muru, iako
bi tada naglasak ostao neobjašnjen (i
je u Ira
bilo
dugo, a u drugom slogu od *Kurrirrissia
kratko).
Moguće
je i da dunavska Karašica i dravska Karašica nisu u antici bili
homofoni, nego da su postali homofoni tek nakon stapanja jera i jora
u hrvatskom jeziku.
Da
se razumijemo, ta rekonstrukcija antičkog imena za Karašicu nije
tvrda znanost. To je kao da pokušavate iz izgovora engleske riječi
pogoditi kako se ista piše. Zapravo, još gore, to je kao da iz
izgovora engleske riječi pokušavate pogoditi kako je glasila
keltska riječ koja je posuđena u staroengleski od koje ta riječ
dolazi. Ustvari, još je gore od toga, jer o keltskim jezicima znamo
daleko više nego o ilirskom jeziku.
Osim
glagola *karr~kurr
u značenju
teći,
mislim
da je u ilirskom jeziku postojala imenica kuros,
s dugim u,
sa značenjem sjever,
da ona dijeli isti korijen kao latinska riječ za sjeverni vjetar,
caurus,
te da od nje dolazi antičko ime otoka Krka, Curicum.
Prihvaćenu tezu da je ilirski jezik pripadao satem
grupi indoeuropskih jezika (kojoj pripada albanski jezik) ja bih
svakako odbacio. Mislim
da su se od indoeuropskog do ilirskog dogodile slične glasovne
promjene kao od indoeropskog do točarijanskog.
Korisnik
Quore zvan
Michal Pietrusinski prigovorio mi je da ja predlažem neočekivane
glasovne promjene kad kažem da „Karašica”
dolazi od *Kurrurrissia,
a da je to osobito problematično jer predlažem da su se iste
neočekivane glasovne promjene dogodile dva puta (i za dunavsku i za
dravsku Karašicu).
Meni nije jasno za koje to glasovne promjene on misli da su
neočekivane, a Quora mi iz nekog razloga ne da da pošaljem komentar
na taj njegov prigovor. Istina, ne smatram se baš nekim stručnjakom
za hrvatsku povijesnu fonologiju, ali, ako sam, recimo, krivo razumio
Havlikov zakon, zašto to nije primijetila dr. sc. Dubravka Ivšić
kad sam joj poslao ranu verziju ovog teksta?
Tako da pretpostavljam da je jedan od razloga zašto
će mnogi odbaciti etimologiju da „Karašica”
dolazi od *Kurrurrissia
to što su „kara
sub”,
a pogotovo „carassius”,
intuitivno slični imenu rijeke „Karašica”,
iako ih je s pogleda povijesne fonologije teško zapravo povezati s
„Karašica”.
*Kurrurrissia
je, kako se meni čini, s pogleda povijesne fonologije trivijalno
povezati s „Karašica”,
ali pretpostavljam da to mnogi neće uočiti.
Korisnik
foruma forum.hr
zvan DarkDivider
kaže da misli da praslavenska fonotaktika nije dopuštala četiri
sloga s poluglasima zaredom (kao što bi bilo u *Kъrъrьsьja).
Nisam siguran je li to istina. Očito je dopuštala tri sloga s
poluglasima zaredom, to se dogodilo u riječi *dьnьsь
(danas).
Otvorio sam pitanje o tome na StackExchangeu.
Nejasno mi je isto tako, ako je to točno,
kako to da glavna struja onomastike izvodi ime Cavtat
od latinskog „(in)
civitate”?
Pretpostavljeni praslavenski oblik posuđen iz latinskog je, koliko
ja to razumijem, *Kьvьtъtь.
Zar ne bismo, ako pretpostavimo da je u praslavenskom postojalo
pravilo da četiri sloga s poluglasima ne mogu biti zaredom, morali
odbaciti i tu etimologiju?
Mogući
prigovor – fonosemantika
Pretpostavljam
da bi mi netko mogao prigovoriti da trebam uzeti u obzir i mogućnost
da to k-r
nije etimološki korijen, već fonosemantički korijen. To jest,
možda su nazivi rijeka na k-r
bivali usvojeni od strane Hrvata ne zato što je to k-r
na nekome jeziku značilo teći,
već zato što je taj zvuk skupine suglasnika (ne nužno povezanih,
ali nekada i povezanih) k-r
Hrvate podsjećao na zvuk koji prave brze rijeke, ili možda na riječ
krv,
ili tako nešto. Nemam pretjerano rigorozan odgovor na to, samo mogu
reći da bi, da je to istina, jezici morali funkcionirati znatno
drugačije nego što se to obično pretpostavlja. Obično se
pretpostavlja da su fonemi od kojih se sastoje riječi potpuno
arbitrarni i nemaju veze sa značenjem riječi, to jest, da
fonosemantički korijeni ne postoje. Evo jedan misaoni eksperiment za
koji mislim da dobro objašnjava zašto:
Pretpostavimo da na nekome jeziku fonosemantički korijen k-l znači
„pokrivati” ili „boja”. Sada, u nekom dijalektu tog jezika
dogodi se glasovna promjena slična Grimmovom zakonu, to jest, tamo
gotovo svako 'k' prijeđe u 'h'. Sada, ako je fonosemantička
hipoteza točna, na tom dijalektu fonosemantički korijen h-l znači
„pokrivati” ili „boja”, te postoji neka sila koja nastoji
spriječiti da se neka riječ od korijena k-l, u značenju
„pokrivati” ili „boja”, posudi iz drugog dijalekta tog
jezika. Primjerice, u engleskom je jeziku postojala nekakva sila koja
je nastojila spriječiti da latinska riječ „color” zamijeni
arhaizam od istog indoeuropskog korijena „hue”.
Mislim da će se većina ljudi složiti da takvih „sila” u jeziku
nema. Iz tog razloga smatram da je etimološki korijen prikladnije
objašnjenje nego fonosemantički korijen.
Uostalom,
meni se čini
da onaj tko prihvati fonosemantičke hipoteze mora odbaciti čitavu
povijesnu lingvistiku. Ako veza između forme i značenja nije
arbitrarna, zašto je onda sistematsko podudaranje glasova između
jezika evidencija da jezici dijele zajedničkog pretka? Teško za
objasniti, zar ne?
Moguć
prigovor - a-priori vjerojatnosti
Jedan
od prigovora koji sam dobio na ovo bio je, kako je napisao korisnik
forum.hr-a
Nyittiuny:
„Radi
li ovo u onomastici? Npr. prema Šimundiću imena Mara, Marcel,
Marčelo, Marena, Margareta, Marin imaju različitu etimologiju iako
svi počinju s MAR. Isto tako s imenima na KAR: Karanfil, Karina,
Karlo, Karmela, Karpoš. A ne bih rekao da su ta imena slučajno
nastala.”.
Mislim da tu ulogu igra a-priori vjerojatnost iz Bayesovog teorema.
Niska
p-vrijednost rezultata eksperimenta za neku hipotezu ne znači mnogo
ukoliko je apriorna vjerojatnost te hipoteze niska, i obratno.
Bayesov teorem glasi: P(A|B)=P(B|A)*P(A)/P(B), gdje P(A|B) označava
vjerojatnost da je A istina pod pretpostavkom da je B istina, a
P(B|A) vjerojatnost da je B istina pod pretpostavkom da je A istina.
Recimo da A predstavlja događaj da je *karr~kurr
na ilirskom značilo
teći,
a da B predstavlja događaj da je rezultat mog eksperimenta
pozitivan. P(A) je apriorna vjerojatnost da je
*karr~kurr
značilo
teći,
a P(A|B) je aposteriorna vjerojatnost toga.
Bayesov
teorem u tom obliku ovdje zapravo ne možemo primijeniti jer bismo za
to morali procijeniti i vjerojatnost da rezultat mog eksperimenta
bude pozitivan pod pretpostavkom da je *karr~kurr
na ilirskom uistinu značilo
teći (to
jest, P(B|A)), a ne znam kako to procijeniti. To je različito od
p-vrijednosti, to jest, vjerojatnosti događaja da rezultat mog
eksperimenta bude pozitivan pod pretpostavkom da *karr~kurr
na
ilirskom nije značilo teći (ona se označava kao P(B|ne(A)) i ona
je ta koja iznosi između 1/300 i 1/17). Recimo da p-vrijednost
iznosi 1/17. Ako uzmemo da P(B|A) iznosi, recimo, 90% (a ne znam kako
to točnije procijeniti, moglo bi biti mnogo manje od 90%, ovo je
samo primjer), onda P(B) iznosi
P(ne(A))*P(B|ne(A))+P(A)*P(B|A)=(1-P(A))*1/17+P(A)*90%. Ako za
a-priori vjerojatnost da je *karr~kurr
značilo
teći
uvrstimo 5%, onda je P(B)=(100%-5%)*1/17+5%*90%=10.1%, a
P(A|B)=90%*5%/10.1%=44.6%. Ako pak za P(A) uvrstimo 20%, tada je
P(B)=(100%-20%)*1/17+20%*90%=22.7%, a P(A|B)=90%*20%/22.7%=79.3%.
Vidimo da na to u što je razumno vjerovati jako utječu ne samo
p-vrijednosti, već i a-priori vjerojatnosti. Naime, ako je apriorna
vjerojatnost 5%, za istu p-vrijednost eksperimenta nije razumno
vjerovati da je rezultat točan jer je aposteriorna vjerojatnost
manja od 50%, a, ako je apriorna vjerojatnost jednaka 20%, onda je
razumno vjerovati.
Imena
ljudi mogu dolaziti odasvud i niotkud. Ljudi mogu biti, recimo,
nazvani po brojevima (što je, izgleda, u antici bio čest slučaj),
nazvani po zanatima, nazvani po biljkama (Ciceron
dolazi od latinske riječi za grašak,
Anton
dolazi
od grčke riječi za cvijet...),
nazvani po životinjama (Alef
je fenička riječ za vola...), nazvani po apstraktnim imenicama
(Dolores
znači patnje
na latinskom...), nazvani po meteorološkim pojavama (Nives
znači snjegovi
na latinskom...)...
Bezbroj riječi su potencijalna imena ljudi. Apriorna vjerojatnost da
su dva imena ljudi koja zvuče slično povezana relativno je mala.
Mislim da će za mnoga osobna imena etimologija zauvijek ostati
misterij. Za rijeke to nije slučaj. Po čemu može biti nazvana
rijeka da bi njezin naziv bio prihvaćen u narodu? Pa, može biti po
riječima za „teći”,
„rijeka”,
„tok”,
imena boja, nazivi nekih riba... Relativno mali broj riječi.
Apriorna vjerojatnost da su imena rijeka koja zvuče slično povezana
relativno je velika, osobito ako su na relativno malom području.
Povezani prigovor koji bih mogao primiti je da, s obzirom na to da
glavna struja hrvatske onomastike smatra da su imena tih rijeka na
k-r nepovezana, apriorna vjerojatnost da su povezana jest jako mala.
Mislim da to nije točno, jer moramo uzeti u obzir da
etimologiziranje kako se obično radi nije nikakav znanstveni
pothvat. Etimologiziranje kako se obično radi ne uključuje nikakvo
eksperimentiranje. Ne možemo općeprihvaćenim etimologijama
pripisivati istu a-priori vjerojatnost kao općeprihvaćenim
teorijama u tvrdim znanostima.
Moguć
prigovor – P-vrijednost je preslaba
Korisnik
PhilosophicalVegan
foruma zvan brimstoneSalad
prigovorio mi je ovako: „Gledaj
Teo, p-vrijednost od približno 1/20 ima smisla za eksperimente. Ali
ti ovdje nisi napravio nikakav eksperiment, ti si samo reanalizirao
postojeće podatke i našao uzorak čija je p-vrijednost 1/17. Za
reanalizu postojećih podataka potrebna je mnogo jača p-vrijednost.
Tebi je privuklo pozornost to što se u nazivima rijeka ponavlja
prefiks od dva suglasnika. Tko zna što bi još privuklo tvoju
pozornost? Vjerojatno bi i prefiks od suglasnika i samoglasnika
privukao tvoju pozornost, pa bi i ponavljanje nekakvog uzorka od
samoglasnika unutar riječi privuklo tvoju pozornost, pa bi i nešto
iz drugih vrsta toponima (a ne samo hidronima) privuklo tvoju
pozornost... Zapravo je iznenađujuće što nisi u nasumičnim
podacima našao prividni uzorak s jačom p-vrijednosti nego 1/17.
Niti p-vrijednost od 1/300 nije pretjerano uvjerljiva, a kamo li
1/17.”.
Mislim da brimstoneSalad
znatno precjenjuje koliko je uzoraka lingvistički plauzibilno da
nisu slučajnosti. Da sam ja tvrdio da se u hrvatskim nazivima rijeka
ponavljaju češće nego što bismo očekivali da je slučajno a-a-i
(kao u Karašica)
i tvrdio da to dokazuje da ti nazivi rijeka dolaze iz istog jezika,
to ne bi bilo plauzibilno. To nije kako jezici funkcioniraju.
Samoglasnici su relativno nestabilni, i ni u jednom poznatom jeziku
ne postoje korijeni od tri samoglasnika s transfiksima od suglasnika
(suprotno nego u semitskim jezicima). Ali ponavljanje prefiksa od dva
suglasnika, kao što je taj k-r uzorak, točno je ono što očekujemo
ako nazivi rijeka dolaze iz istog jezika.
Moguć
prigovor – Je li taj k-r uzorak u nazivima rijeka ograničen na
mjesta gdje se govorio ilirski?
Još
jedan prigovor koji sam primio jest, kako je rekao Zrcadlo
na Tapatalk forumu Istorija Balkana: „Meni
se čini da ti impliciraš da je to k-r što se pojavljuje u nazivima
rijeka ograničeno na prostore gdje se govorio ilirski jezik. A čini
mi se da to nije istina. Na granici Srbije i Rumunjske postoji rijeka
koja se zove Karaš. Tamo se nije govorio ilirski jezik, tamo se u
antici govorio tračanski jezik. A, koliko ja znam, doslovno se svi
lingvisti koji su proučavali ostatke tračanskog jezika slažu da je
on pripadao Satem grupi indoeuropskih jezika. Tako da naziv Karaš ne
možemo izvoditi od indoeuropskog *kjers.
Ne vidim zašto onda pretpostaviti da se nazivi tih rijeka u
Hrvatskoj mogu.”.
Mislim da bismo, dok netko ne dokaže da je p-vrijednost tog k-r
uzorka u Rumunjskoj uistinu mala, trebali pretpostaviti da imena
Karaš
i Karašica
nisu povezana. Dok netko ne izračuna tu p-vrijednost, pozivanje na
hidronime na k-r u Rumunjskoj je korištenje anegdotalne evidencije,
a ne znanost.
Sličan
prigovor dala mi je i korisnica forum.hr-a zvana karizmavjere.
Po njoj, da je moja teorija da oko 6% naziva rijeka dolazi od *kjers
točna, očekivali bismo da u Srbiji (gdje su se u antici govorili
dačanski i tračanski jezik, za koje se svi lingvisti slažu da su
bili satem jezici) postoje mnoge rijeke na s-r.
A na engleskoj Wikipediji postoji popis od oko 60 velikih rijeka u
Srbiji, i nijedna od njih ne počinje na s-r. Kako kaže
karizmavjere,
vjerojatnost da se to dogodi slučajno iznosi 2.5%. Moj odgovor na to
bi bio: Imate li vi neku teoriju koja ne pati od tog problema?
Mainstream lingvistika tvrdi da je *ser
bila praindoeuropska riječ za teći,
pa bismo taj isti argument mogli koristiti i protiv mainstream
lingvistike, zar ne?
Moguć
prigovor – Je li moj rad povratak na devetnaestostoljetne ideje o
povijesnom determinizmu?
Korisnik
Reddita phonotactics2
komentirao je da se njemu čini da je moj rad povratak na
devetnaestostoljetne ideje o povijesnom determinizmu, idejama kao što
je Marksizam, da su društvene pojave predvidive i da slijede
određene zakonitosti.
Iskreno,
ja baš ne razumijem kako netko to može misliti. Je li itko sumnja
da su glasovne promjene koje opisuje Grimmov zakon daleko
vjerojatnije nego glasovne promjene suprotne od onih koje opisuje
Grimmov zakon? Je li reći to nekako povijesni determinizam usporediv
s Marksizmom?
A
i ne vidim kako to moj argument ima skrivenu premisu da je ikakva
verzija povijesnog determinizma istinita. Ja koristim podatke iz
sadašnjosti da bih odredio prošlost, a ne budućnost.
Moguć
prigovor – Jesam li ja kao Joseph Greenberg kad kontradiktiram
prihvaćenoj metodologiji istraživanja toponima
Pretpostavljam
da bi se nekome moglo učiniti da sam ja poput Josepha Greenberga i s
njime povezanim ljudima koji tvrde da su rekonstruirali prvi ljudski
jezik (kako ih oni zovu, globalne etimologije). No mislim da postoji
velika razlika između onoga što ja tvrdim i onoga što Joseph
Greenberg tvrdi. Joseph Greenberg u biti tvrdi da nam lingvistička
tipologija (koje su glasovne promjene vjerojatne, a koje nisu)
omogućava da idemo dublje u prošlost i brže nego što nam
omogućava tradicionalna komparativna metoda. Drugim riječima, on
tvrdi da je našao prečicu. Ali njegovo je etimologiziranje zapravo
povratak na srednjovjekovno look-and-guess etimologiziranje, i
nekompatibilno je s komparativnom metodom (da se njegove metode
primijene na indoeuropske jezike, koji su rigorozno proučavani, dale
bi ogromnu količinu false-positivea). Zato njegove metode ne mogu
zapravo biti, kako on tvrdi, prečica. Ja ne tvrdim da sam našao
prečicu. Ja tvrdim da je općeprihvaćena metoda proučavanja
toponima (ako se ona uopće može zvati metodom, jer mislim da ona
nije ni približno toliko jasno definirana kao što je komparativna
metoda) neopravdana i nekompatibilna s teorijom informacija, jer je
dala rezultate koji su po teoriji informacija nevjerojatni.
Moguć
prigovor – Je li kolizijska entropija imenica u hrvatskom jeziku
znatno manja nego kolizijska entropija svih riječi u rječniku?
Korisnik
Reddita neuralbeans
ima sljedeći prigovor na moj rad (pisao je na engleskom): „Možda
je kolizijska entropija imenica u hrvatskom jeziku znatno manja nego
kolizijska entropija svih riječi u Aspellovom rječniku za hrvatski
jezik. Pogledaj, recimo, shvahilski jezik. Svahilski jezik ima 18
rodova imenica koji se razlikuju po prefiksima. Tamo je kolizijska
entropija imenica očito manja od kolizijske entropije svih riječi u
rječniku, jer parovi suglasnika kojima mogu počinjati ostale riječi
u jeziku imenice ne mogu počinjati. Trebaš provjeriti da isto nije,
makar u manjoj mjeri, istina i za hrvatski jezik. Hidronimi su
imenice, i trebaš ih uspoređivati s ostalim imenicama, a ne sa svim
riječima u rječniku.”.
U biti, suprotno od onoga što mi je odgovorio dr. sc. Franjo Jović
(jer dr. sc. Franjo Jović misli da na morfologiju ne odlazi mnogo
entropije, a neuralbeans
misli da na morfologiju odlazi nerazmjerno mnogo entropije u
imenicama). Mislim da je taj prigovor u biti sličan Al
Dente-ovom
prigovoru. Nije na meni da radim još koji eksperiment da bi se
nekoga uvjerilo, a osobito ne kompliciraniji eksperiment. Nije očito
kako odrediti kolizijsku entropiju suglasnika samo u imenicama. I
nije jasno zašto bismo očekivali da je ona manja nego kolizijska
entropija svih riječi u Aspellovom rječniku. Zar nije barem toliko
vjerojatno da je veća?
Neuralbeansova
hipoteza
tipična je ad-hoc hipoteza: izmišljanje razloga zbog kojih
eksperiment ne bi funkcionirao. I nije na meni da radim neki
komplicirani eksperiment zbog nečije ad-hoc hipoteze. I to što
neuralbeans
može naći nekakvo teorijsko opravdanje za svoju ad-hoc hipotezu ne
čini je vjerojatnom. Lagano je naći teorijsko opravdanje za ad-hoc
hipotezu, pogotovo u mekanim znanostima kao što je lingvistika.
Naravno,
moguće
je da sam u krivu. Moguće je da istraživanja uistinu pokazuju da je
kolizijska entropija imenica znatno manja od kolizijske entropije
preostalih riječi u rječniku. Otvorio sam pitanje o tome na
par internetskih
foruma
.
Moguć
prigovor – jesam li ja kao oni lingvisti koji su prije Michaela
Ventrisa pokušavali statističkim metodama dešifrirati Linearno B
pismo
Korisnik
forum.hr-a
zvan karizmavjere
prigovorio mi je da ga moj rad podsjeća na sve one lingviste koji su
pokušavali statističkim metodama dešifrirati Linearno B pismo, da
bi ga na kraju samouki lingvist Michael Ventris dešifrirao
„tradicionalnim”
metodama. Ja baš i ne vidim poveznicu. Lingvisti prije Michaela
Ventrisa uglavnom su koristili statističke metode prilagođene
alfabetima, a ne silabičkim pismima kakvo je Linearno B. Također,
većina njih je pretpostavila da je jezik pisan Linearnim B pismom
etrurski, a ne grčki, što je dodatno dezinformiralo tadašnje
primitivne statističke metode. Naime, ako pokušate statističkim
metodama dešifrirati alfabet kojim je pisan hrvatski jezik, a
pogrešno pretpostavite da je njime pisan engleski jezik, vjerojatno
ćete za najčešći znak pretpostaviti da je e,
a zapravo je najvjerojatnije i
(najčešće slovo u hrvatskom jeziku). Ja ne vidim da ja ovdje radim
takve neopravdane pretpostavke.
Moguć
prigovor – impliciram li ja da nazivi životinja krava
i krpelj
dolaze od ilirske riječi za teći
Korisnik
forum.hr-a
zvan judolino
prigovorio mi je da se njemu čini da ja impliciram da nazivi
životinja krava
i krpelj
dolaze od ilirske riječi za teći,
a da je to očito apsurdno. I mnogi drugi na tom forumu davali su mi
slične prigovore. Meni nije jasno kako ide taj argument. I kad sam
judolina
pitao da mi to pojasni, on mi nije odgovorio. Mislim da se svatko tko
je proučavao hrvatske toponime slaže da je to s-r
što se ponavlja u hrvatskim toponima (Serapia,
Serota, Sirmium...)
ilirska riječ za teći,
a mislim da to ni najmanje ne sugerira da ime životinje srna
dolazi od te riječi.
Je
li ilirski jezik pripadao
centum
ili satem
grupi indoeuropskih jezika
Napomena:
Kad sam ovaj tekst objavljivao u Valpovačkom
godišnjaku, recenzenti su me natjerali da ovu raspravu o tome je li
ilirski bio centum ili satem izbacim.
Probajmo,
da bismo bili objektivniji, navesti argumente za i protiv toga da je
ilirski bio centum
jezik, to jest, da u njemu indoeuropsko kj
prelazilo u k.
Argumenti za to bili bi, recimo:
Imena
mnogih rijeka gdje se govorio ilirski jezik počinju s
k(+samoglasnik)+r,
što bi moglo dolaziti od indoeuropske riječi za konja, *kjers,
odakle u keltskim jezicima i u latinskom jeziku dolaze riječi sa
značenjem trčati
(a
nije teško zamislivo da bi od značenja trčati
kasnije
proizašlo značenje teći).
P-vrijednost iznosi negdje između 1/300 i 1/17. Protuargumenti
protiv ovog argumenta mogli bi biti da nije općeprihvaćeno da su
ta imena rijeka uistinu povezana (što će se možda uskoro
promijeniti), te možda da je izvođenje riječi za teći
od riječi sa značenjem konj
neuvjerljivo.
Mnogi
natpisi na ilirskom jeziku počinju s „klauhi
zis”,
što je, po svemu sudeći, značilo „Usliši
bože (ovu molitvu)”,
dakle, riječ „klauhi”
dolazila bi od indoeuropskog *kjlew
(čuti, uslišiti). Ovdje nije očito kako izračunati p-vrijednost.
Protuargument je, naravno, da u mnogim satem
jezicima (u kojima kj
prelazi u s)
postoji iznimka za kj
ispred likvida l
i r,
a da je među njima i albanski jezik.
Ako
pretpostavimo da je ilirski jezik centum
jezik, ime Krk
može se čitati kao sjeverni,
od indoeuropskog *(s)kjeh1weros,
odakle dolazi latinska riječ caurus
za sjeverni vjetar. Ponovno, nije očito kako izračunati
p-vrijednost. Protuargument bi, ja pretpostavljam, bio da -icum
i -icta,
sufiksi s kojima se ime Krk
pojavljuje u antičkim povijesnim izvorima, nisu tipični
indoeuropski, pa da onda nije logično pretpostaviti da je ime Krk
indoeuropskog podrijetla.
Ako
pretpostavimo da je ilirski jezik centum
jezik, ime Incerum,
današnja Požega, može se čitati kao srce
doline.
Od *h1eyn
(dolina) i *kjer(d)
(srce). Nije
očito kako ovdje izračunati p-vrijednost.
Ako
pretpostavimo da je ilirski jezik centum
jezik, ime Cibelae,
današnji Vinkovci, može se čitati kao jaka
kuća,
to jest, utvrda.
Od *kjey
(kuća, odatle latinski civis)
i *bel
(snažan, odatle korijen u latinskom debilis)
Nije
očito kako ovdje izračunati p-vrijednost. Protuargument bi mogla
biti hipoteza
Antuna Mayera da
je ime Cibelae
srodno
grčkoj riječi κεφαλη (glava), jer u mnogim jezicima riječ
za brežuljak dolazi od riječi za glavu. Ali problem s tom
etimologijom,
kako objašnjava
Dubravka Ivšić na 136. stranici svog doktorata, to je što
današnja lingvistika grčku riječ za glavu izvodi od indoeuropskog
*ghebh,
da je u grčkom riječ počinjala na χ, pa da je on prešao u κ po
Grassmannovom zakonu (koji, u biti, kaže da ako se dva h
nađu preblizu, prvo od ta dva h
ispada). Zašto bi u ilirskom Cibelae,
ako stvarno dolazi od *ghebh,
počinjalo na k,
a ne na g?
Argumenti
protiv toga da je ilirski bio centum
jezik, to jest, argumenti da je ilirski bio
satem
jezik, koji se obično navode, jesu:
Albanski
jezik je satem
jezik. Protu-argument je, naravno, kako znamo da je albanski jezik
blisko srodan ilirskome? I,
naravno, nije očito kako izračunati p-vrijednost.
Antičko
ime za Podgoricu u Crnoj Gori bio je Birziminium,
a današnje ime Podgorica
je onda vjerojatno prijevod tog imena, a Birz-
vjerojatno dolazi od indoeuropskog *bhergjhs
(brdo). Skrivena premisa u tom argumentu je da se z
u Birziminium
izgovaralo z,
što je nevjerojatno. U antici je z
u latinskom jeziku označavao, u biti, bilo koji afrikat koji ne
postoji u latinskom jeziku, prije svega grčko dz.
U tom pogledu, zar nije vjerojatnije da se to ime izgovaralo nešto
kao Birdžiminium,
te da je riječ o sekundarnoj palatalizaciji? Možda je u ilirskome
-rgi-
prelazilo u -rdži-,
ili tako nešto. P-vrijednost, naravno, opet nije očito kako
izračunati.
Antičko
naselje na ušću rijeke Vrbas u Savu zvalo se Osseriatis,
a tamo ima mnogo jezera, pa bi to ime moglo biti povezano s
hrvatskom riječju jezero.
P-vrijednost je, naravno, opet neizračunljiva. Ispravan
protu-argument, po meni, bio bi: Zar nije barem toliko vjerojatno da
je -ser-
u Osseriatis
povezano sa ser-
u imenima Serapia
(rijeka Bednja),
Serbinum
(Gradiška) i
Serota
(Virovitica)? Zar
ne bi Osseriatis
moglo značiti „utjecanje
(jedne rijeke u drugu)”?
Također,
ako je riječ jezero
uistinu indoeuropskog podrijetla, da ima svoj odraz u ilirskome,
zašto je nema u zapisanim starim indoeuropskim jezicima?
Ilirska
riječ za broj pet, potvrđena na nekim natpisima, bila je penkaheh,
od indoeuropskog *penkwe,
a *kw
je u centum jezicima obično ostajalo (kao u latinskom quinque),
dok je u satem jezicima prešlo u 'k'.
Opet,
nije očito
kako izračunati p-vrijednost. Protuargument bi mogao biti da se
prelazak svakog *kw
u 'k'
dogodio i u točarijanskom jeziku, a on je bio centum jezik.
Povezani
argument mogao bi biti da je općeprihvaćena etimologija da je ime
Colapis,
antičko ime za rijeku Kupu, na ilirskom jeziku značilo krivudava
voda,
da je col
značilo krivudav
i da dolazi od korijena *kwel
(vrtjeti
se,
odatle *kwekwlos,
kotač),
da je ap
značilo voda
i da dolazi od korijena *h2ep
(voda)
i da je -is
latinski nastavak, te da je i tamo *kw
prešlo u k,
ali to je još slabiji argument (etimologiziranje toponima daleko je
manje sigurno nego etimologiziranje naziva brojeva).
Paul
Kretschmer koristio je sljedeći
argument za to da je ilirski jezik bio satem
jezik: „U ilirskom je jeziku kratko o
prelazilo u a.
Prelazak kratkog o
u a
koreliran
je s prijelazom /c/ (glasom koji se u indoeuropeistici obično
označava sa *kj)
u /s/. Dakle, ilirski je vjerojatno bio satem
jezik.”.
Nisam uvjeren da je ijedna od tih dviju premisa istinita. U vezi s
prvom premisom, očito je da se kratko o
barem nekada održalo kao
o u
ilirskom jeziku, kao u hidronimu Colapis.
Istina je da je glas a
čest u ilirskim nazivima rijeka, kao što su Drava i Sava, i da se
to može tumačiti kao da dolaze od ranijeg *Drova
(drugi ablaut korijena *drew,
prodirati)
i *Sova
(drugi
ablaut korijena *seh1u,
mokar),
ali zar nije barem toliko vjerojatno da je u ilirskoj gramatici
postojao a~u
ablaut, nego
da je postojala glasovna promjena da kratko o
prelazi u a?
Štoviše, zašto bi o
u *Sova
bilo kratko, ako to dolazi od *seh1u?
Meni se čini da je ablaut ovdje bolje objašnjenje od glasovne
promjene. U vezi druge premise, ima li on neku statističku analizu
koja bi tu premisu dokazivala? Gotovo sam siguran da ne. Očito je
da to da kratko o
u
a
prelazi ako i samo ako *kj
prelazi
u s
nije bezizniman zakon lingvistike: to se dogodilo u njemačkom
jeziku u riječi za broj osam, acht,
a tamo je *kj
prelazilo
u h.
Ako ćete tvrditi da je nešto vjerojatno, bilo bi dobro da imate
izračun koji pokazuje kolika je ta vjerojatnost uistinu. Paul
Kretschmer to, meni se čini, nema.
Sve
u svemu, čini mi se da se po pitanju je li ilirski bio centum
ili satem
jezik može napraviti samo jedan znanstveno rigorozan argument
(kojemu se može izračunati p-vrijednost), i da je on za to da je
ilirski jezik bio centum
jezik. Dr. sc. Dubravka Ivšić
e-mailom mi je odgovorila da misli da je moguće da je oboje točno,
da ilirski jezik nije bio jedan jezik, već zajednički naziv za
indoeuropske jezike koji su se govorili na ovim prostorima, a koji
međusobno nisu bili blisko srodni. Ja bih na to odgovorio ovako:
„Što
očekujemo ako neka skupina toponima dolazi iz istog jezika?
Očekujemo ponavljanje istih ili sličnih elemenata u nekom značenju.
I to je upravo ono što vidimo s tim k-r uzorkom.”.
Da se u hrvatskim nazivima rijeka ponavljaju samo elementi koji se
trivijalno daju objasniti indoeuropskim korijenima, kao što su
ser
(od korijena *ser
koji je značio upravo
teći)
ili
ap
(od *h2ep,
što je značilo upravo voda),
možda bi ideja da je ilirski jezik zapravo bio mnogo međusobno
daleko srodnih indoeuropskih jezika i dolazila u obzir. Tada bismo
mogli reći „Možda
su mnogi ilirski jezici zadržali te korijene nepromijenjene.”
(zajednički arhaizmi). Ali činjenica je da se taj k-r element
ponavlja daleko češće, a ne da se tako trivijalno objasniti
indoeuropskim korijenima. Za taj k-r element daleko je bolje
objašnjenje da je ilirski jezik bio jedan jezik. Naravno, uvijek
možemo raditi ad-hoc hipoteze (zajedničke inovacije,
posuđenice...), ali ovdje bi trebalo biti očito što je razumno
objašnjenje, a što ad-hoc hipoteza. Također, kao znanstvenici,
moramo se zapitati je ta ideja, da ilirski jezik nije bio jedan
jezik, falsifijabilna. Meni se čini da nije.
Mogući
prigovor – bugarska dijalektalna riječ „kariti” za „teći”
Jedan
moj prijatelj iz stvarnog života, koji je također toponimijski
entuzijast, rekao mi je da se slaže sa mnom da su moji izračuni
vezani za teoriju informacija vjerojatno točni i da je *karr~kurr
bila ilirska riječ za teći i da Karašica dolazi od ilirskog imena
sličnog *Kurrurrissia, ali se ne slaže sa mnom da je najbolje
objašnjenje za tu riječ *karr~kurr
da
je ilirski bio centum jezik i da ta riječ dolazi od *kjers.
On je uvjeren da je negdje pročitao da u nekim bugarskim dijalektima
postoji riječ kao „kariti” koja znači „teći” i da se
pretpostavlja da je ona tračanskog podrijetla. A tračanski je,
naravno, bio satem jezik. To ima daleko više smisla ako
pretpostavimo da su tračanski i ilirski bili blisko srodni jezici
nego ako pretpostavimo da je ilirski bio neki centum jezik.
Ja
ni uz najbolju volju nisam uspio naći na internetu nikakve
informacije o bugarskoj dijalektalnoj riječi „kariti” sa
značenjem teći.
Mogući
prigovor – zašto 'r' u ranim potvrdama imena „Karašica” nije
geminirano
Na
jednom internetskom forumu primio sam prigovor da se konsonantizam
trinaestostoljetne potvrde „Karassou” ne može objasniti mojom
etimologijom, jer bismo očekivali da je 'r' u 13. stoljeću bilo
udvostručeno (geminirano). Naime, da su u hrvatskom jeziku nakon
Havlikovog zakona postojali geminati koji su nastali tako što je
slabo jer ili slabo jor bilo između dva jednaka suglasnika, a da su
ti geminati tek kasnije izgubljeni, nakon 13. stoljeća. Otvorio sam
pitanje o tome na StackExchangeu.
Brojanje
do deset na ilirskom jeziku
Napomena:
Natjerali su me urednici Valpovačkog godišnjaka da i ovaj ulomak
eksciziram. Bog te pitaj zašto!
Evo
kako bih ja rekonstruirao brojeve od jedan do deset na ilirskom
jeziku:
Indoeuropski
|
Ilirski
|
Napomena
|
*h1oinos
|
*inos
|
Pretpostavljam da je *oi
prelazilo u dugo 'i',
kao što je *ew prešlo u dugo 'u'
u *kuros (prvi
samoglasnik u dvoglasniku se gubi, a drugi se produžava).
|
*dwoh1
|
*do
|
*wo
prelazi
u dugo 'o',
iz istog razloga zašto *oi
prelazi u dugo 'i'
|
*treis
|
*tris
|
*ei prelazi u
dugo 'i',
iz istog razloga zašto i *oi
prelazi. Tako i i u
Cibelae
dolazi od *kjey-bel
(nejasno je zašto se l
nije udvostručilo).
|
*kwetwores
|
*kettores
|
*t se geminira jer dolazi nakon kratkog
suglasnika. Naime, kao što sam napisao na već više mjesta,
mislim da je u ilirskom vrijedio zakon da svi slogovi moraju biti
jednake duljine, te da se to postizalo geminiranjem suglasnika
nakon kratkog samoglasnika (kao što je neko vrijeme bilo u
engleskom jeziku, te da zato ima dva 's'
u Issa,
jer je 'i'
kratko).
|
*penkwe
|
*penka
|
Pretpostavljam da je -heh
u potvrđenoj riječi penkaheh
bio
neki gramatički nastavak. Prijelaz iz krajnjeg *e
u 'a'
je nejasan.
|
*swekjs
|
*seks
|
|
*septm
|
*septim
|
Samoglasno *m
prelazi
u im,
kao što *h1n
(dolina) prelazi u *in
u Incerum
(srce doline).
|
*h3ekjtow
|
*oktu
|
|
*h1newn
|
*ennun
|
Smatram da je početno h
(laringeal) barem nekada prelazilo u 'e'
u
Ilirskom, te da odatle dolazi početno
'e'
u hidronimima Ervenica
i Ervenik
(od *h3rews,
teći, isti korijen kao latinski ruere).
*ew,
naravno, prelazi u dugo 'u', kao i u *kuros
(sjever).
|
*dekjm
|
*dekkim
|
|
Od
tih rekonstrukcija, rekonstrukciju da je *penka
bila riječ za broj pet smatram najsigurnijom.
Tvorba
riječi u ilirskom jeziku
Izgleda
da je iznimno produktivan način tvorbe riječi u ilirskom jeziku bio
tako da se na glagolski korijen doda imenički korijen i onda se
opcionalno doda sufiks. Na taj su način tvoreni toponimi Ser-ap-ia
(teći-voda-sufiks),
Col-ap-is
(krivudati-voda-sufiks), Bal-issa
(vreti-izvor), *Kurr-urr-issia
(teći-voda-sufiks)... Koliko znam, jedina iznimka je Ci-bel-ae
(kuća-biti jak-sufiks), gdje imenica ide prije glagola.
Je
li moja teorija falsifijabilna
Po
Karlu Popperu, kao i većini današnjih filozofa znanosti, glavna
razlika između znanosti i pseudoznanosti je falsifijabilnost. Kako
je to Daniel Ross, moderator foruma linguistforum.com,
objašnjavao FlyingRedSportsCaru,
korisniku koji je zastupao neku fonosemantičku hipotezu, „Zamisli
da je tvoja teorija kriva. Zašto
bi bila kriva? Kako bismo to znali?”.
Pa, mogu se sjetiti nekoliko razloga zašto bi moja teorija bila
kriva:
Možda
bi neki prikladniji model jezika sugerirao da taj k-r
uzorak u hrvatskim hidronimima nije statistički značajan.
Korištenje rođendanskog paradoksa i kolizijske entropije ovdje se
čini kao prirodan izbor, ali možda ima bolji. Možda bih, da sam,
recimo, računao nekako preko Markovnikovljevog lanca (ili nekog još
boljeg modela jezika) dobio znatno veću p-vrijednost. To mi se čini
nevjerojatno, jer su ovaj tekst pregledala dva doktora teorije
informacija (Franjo Jović i Anđelko Lišnjić) i još nekoliko
ljudi koji znaju o teoriji informacija daleko više nego što ja
znam, pa tako nešto nisu primijetili. Ali nije nemoguće.
Možda
se taj uzorak da se k-r
ponavlja
u nazivima rijeka pojavljuje i na području gdje se ilirski jezik
nije govorio. U tom je slučaju bezpredmetno pripisivati taj k-r
uzorak ilirskom jeziku, i vjerojatno ga treba pripisivati
predindoeuropskom jeziku.
Možda
je neka fonosemantička hipoteza istinita. U tom je slučaju moja
metodologija loša. Ali onda je isto tako i komparativna metoda
rekonstrukcije prajezika loša.
Možda
neki povijesni izvor nedvosmisleno kaže da je Karassou
na nekom jeziku koji se ovdje govorio značilo crna
voda
ili sjeverna
voda.
U tom slučaju objašnjenje s turkijskim nije toliko neosnovano kao
što se sada čini.
U
svakom slučaju, ne čini mi se da moja teorija nije falsifijabilna.
Ostali
upadljivi uzorci u nazivima mjesta u Hrvatskoj
Za
taj uzorak da imena rijeka u Hrvatskom počinju sa k-r relativno je
jednostavno procijeniti p-vrijednost. Uočio sam još nekoliko
uzoraka u hrvatskim nazivima mjesta za koje nije očito kako
procijeniti p-vrijednost, iako mi se čini da bi mogla biti mala.
Recimo, izgleda da je *issa~iasa
na ilirskom jeziku značilo nešto kao „izvor
ljekovite vode”.
Antički naziv za Daruvar bio je „Balissa”,
i tamo su bile jedne od najvećih rimskih termi na ovim prostorima.
Antički naziv za Varaždinske Toplice bio je „Iasa”.
I je li moguće da je antičko ime otoka Visa, Issa,
isprva
označavao onaj izvor zapadno od rimskih termi na koji su se te
velike terme napajale?
Kolika je vjerojatnost da se taj uzorak dogodi slučajno? Ako nije
slučajno, etimologija je jasna: to dolazi od indoeuropskog korijena
*yes
(vreti), kao što hrvatska riječ vrelo
dolazi od glagola vreti.
Ono
„Bal”
u „Balissa”
moglo bi dijeliti isti korijen kao latinski riječ za
vreti,
„bullire”,
koja je nejasne etimologije. Također mislim da je moguće, ako ne i
vjerojatno, da su Iliri vjerovali da je onaj izvor u Jozincima kod
Donjeg Miholjca ljekovit, te da ime Jozinci dolazi od ilirskog imena
*Iasona.
Još
jedan uzorak
u hrvatskim nazivima mjesta koji upada u oči je
da imena morskih otoka često počinju sa l-s:
današnje talijansko ime za Hvar je „Lesina”,
današnje talijansko ime za Vis je „Lissa”,
postoje dva otoka koja nose ime „Lošinj”,
a antičko ime za otok Ugljan isto je bilo „Lissa”
(kod Plinija u Naturalis Historia, 3. svitak, 63. poglavlje, „Contra
Iader est Lissa.”,
Nasuprot
Zadru je Lissa).
Kolika je vjerojatnost da se to dogodi slučajno? Ako nije slučajno,
koja bi mogla biti etimologija? Ne znam odgovore na ta pitanja.
Zaključak
Iz
moje perspektive, čini se tužnim što toliko malo znamo o jezicima
koji su se na ovim prostorima govorili, te iz kojih, nesumnjivo,
dolaze bezbrojni današnji toponimi. Za toliko jezika znamo da su
postojali, a na njima ne znamo ni do deset nabrojati (ni za etrurski
jezik, recimo, nismo sigurni je li huth
značilo
četiri,
a ša
značilo šest,
ili obrnuto, a nismo sigurni ni je li šar
značilo deset
ili je značilo dvanaest,
a da je možda halch
značilo deset).
Kako je korisnik Reddita Qafqa
rekao, i mislim da je dobro rekao: „Nac
avil pulumchva falatul snuiaph, aca Rasnal amuce ziv, nanatnam ica
cnara.”
(Već onoliko godina koliko ima zvijezda na nebu, etrurski je jezik
mrtav, i nitko ga ne razumije.). Iliri su nam na svom jeziku ostavili
nekoliko stotina natpisa, ali to su, uz malobrojne iznimke, natpisi
od svega nekoliko riječi. Hvala Bogu, pisani su grčkim alfabetom,
pa te riječi možemo izgovoriti. Ali nijedan od tih natpisa nije
bilingvalan, da možemo biti sigurni što su točno te riječi
značile. Zašto se baš nitko nije sjetio to napraviti? Zar nisu
pomislili da bi nekoga nakon dvije tisuće godina zanimalo što ti
natpisi znače? Zar su mislili da njihov jezik neće umuknuti? Ili ih
nije bilo briga? I u povijesnim tekstovima rijetko kad je netko
umetao prijevode pojedinih riječi ili fraza iz tih jezika. I za
ilirski se jezik barem dva puta dogodilo da dva autora spomenu upravo
istu riječ. Etimologija da je Brač
bila ilirska riječ za jelena općeprihvaćena je zato što ju je u
6. stoljeću predložio Stjepan Bizantski, zato što je Strabon u 1.
stoljeću prije Krista, u 6. svitku u 3. poglavlju Geografije,
predložio da ime talijanskog gradića Brindisi dolazi od ilirske
riječi za jelena jer zaljev u kojem se on nalazi oblikom podsjeća
na glavu jelena, te zato što je današnja latvijska riječ (jer je
latvijski jedan od najarhaičnijih današnjih indoeuropskih jezika)
za jelena briedis.
Amijan i Jeronim oboje su spomenuli da je sabaium
ilirska riječ za pivo. Četiri autora, svega dvije riječi. Upitno
je trebamo li čuvati male jezike i dijalekte: troškovi očuvanja
jezika su veliki i nerijetko idu upravo na najsiromašnije ljude u
društvu. No nije upitno da ih trebamo dobro dokumentirati za buduće
generacije. Da su antički povijesničari dobro dokumentirali ilirski
jezik, ne bi bilo ovakvih nedoumica.


